Tag: Problem solving

Ratio, Quidditch, and Stimming 

My second grade gifted students are very excited about reading Harry Potter. A couple boys talk about the books often. I’ve had to stop them before they give away any of the plot and spoil the literary experience for those who haven’t read as much. 

Caught being classy; These 2nd graders are finishing up “Who Would Win” books comparing insects.

The other day one of my students was pacing around the room conducting a monologue about quidditch. Everyone was working on wrapping up an end of the year project when this student took a break to stim. 

Over the years I’ve had a few students who stim. It took me a while to understand what this was, and even longer before I was familiar with the term. Stimming is an abbreviation for stimulation. It is when a person uses sound, motion, touch, or other stimulating sensations to soothe the spirit. A person may sing to themselves, wave their hands, repeatedly run their fingers over a piece of fabric, or pace the floor. It usually involves repetition.

The National Autistic Society suggests four reasons a person may stim. They could be using their stim to self-regulate the amount of sensory input they are receiving. By making their own noise, they are blocking out other sounds. Flapping one’s hands or pacing the floor puts the stimming person in charge of what their mind thinks about. It can be a way of dealing with stress and anxiety. Sometimes, a stim can just be enjoyable. Finally, there are times when people who stim do it in order to produce sensory input. Maybe their mind needs something to do, so they stim. 

Stimming can sometimes be distracting for other students in the classroom. It is best for everyone to understand that this is a completely natural and necessary thing for some people. 

I’ve grown accustomed to my 2nd grade stimmer. When he started talking about quidditch to no one in particular, I just let him pace and say his soliloquy. He was going over the rules for the game, and something he said got me thinking. He mentioned the golden snitch, and said that catching it would win you the game. I didn’t mean to be contrary, but I interrupted his stimming to ask, “Do you automatically win if you catch the snitch?” 

He paused his pacing and thought for a moment before explaining, “It is worth 150 points, so whoever catches it will most likely win.” That was a very good answer, but I saw an opportunity for a mini math lesson, that ended up turning into an awesome math lesson!

Another student chimed in, “Catching the snitch ends the match.” 

“But does it guarantee a win?” I challenged. 

The group thought about it for a second. The quidditch expert conceded that, “No. Catching the golden snitch doesn’t mean you win.”

In order to stretch their thinking and prove my point, I suggested they figure out how many scores the other team would have to make in order to win against a team that caught the snitch. Hardly a second passed before the quidditch expert told me the answer; sixteen. 

With each score producing ten points, sixteen would mean that the team without the snitch would have ten more points (160) than the snitch-catching team. “But, it is pretty unlikely that one team would score sixteen goals while the other didn’t earn even one,” I suggested. “What if the team that didn’t catch the snitch was twice as good. For every goal the snitch-catchers earned, the other team scored two. Then, how many goals would have to be scored in order to win without catching the snitch?”

I drew a T chart on the whiteboard. I wrote “Team A” on one side of the T and “Team B” on the other. At the bottom of  Team B’s column I wrote 150 and labeled it, “Golden Snitch.” I then wrote a two directly under Team A and a one under Team B. I explained that Team A scored two goals while Team B only scored one. “How many points does each team have?”

When the second graders told me that Team A had twenty points while Team B had ten, I commended them for multiplying the number of scores by ten, the value of each goal. Only, that was not accurate. I pointed to the “150” at the bottom of Team B’s column. “Team B actually has 160 points,” I told them. 

I wrote another “two” under Team A and an additional “one” under Team B. “Now how many points does each team have?” At this point it was forty to 170. We kept doing this until Team A’s score crept closer and closer to Team B’s. It took a few minutes to calculate, but my students were riveted to the math. Once Team A earned enough points to overcome the snitch catchers, I restated my original query: “How many goals did Team A need to score inorder to beat the team that caught the snitch?” 

They skip-counted to find the answer. I showed them that they could have multiplied the number of twos by two and get the same answer. I also explained to them that the idea of a team being twice as good as another is a ratio. I wrote 2:1 above the T chart. “This means Two to One,” I told them. “For every two goals that this team scored…” I pointed to Team A, “The other earned only one goal.” I left it at that. Our time was up, and they had consumed enough new terms and problem-solving for the morning. 

As you can see, there was a lot of math going on! Among other things, we figured out the difference between the teams to see how far we had to go for Team B to overtake Team A. The challenge was to find out the smallest number of goals necessary to win without getting the snitch.

I was so pleased with the spur of the moment lesson that I decided to reuse it when my fourth graders joined me. I wrote the question, along with some quidditch facts, on a Google Jamboard. A couple of fourth graders engaged in drawing on the picture of Harry and writing some random thoughts. I’ve found that letting students do this allows them the freedom to think creatively. This could very well be a form of stimming. 

I guided their work by asking the question verbally. I retaught the concept of ratio, which I had introduced earlier in the year. The fourth graders were much faster at figuring out the answer. They immediately guessed thirty goals might push Team A over the edge of victory. I wrote “30” under Team A, and asked how many goals Team B would earn with a ratio of two to one. They accurately told me fifteen. We multiplied both numbers by ten and added the snitch to Team B’s score: Tie. 

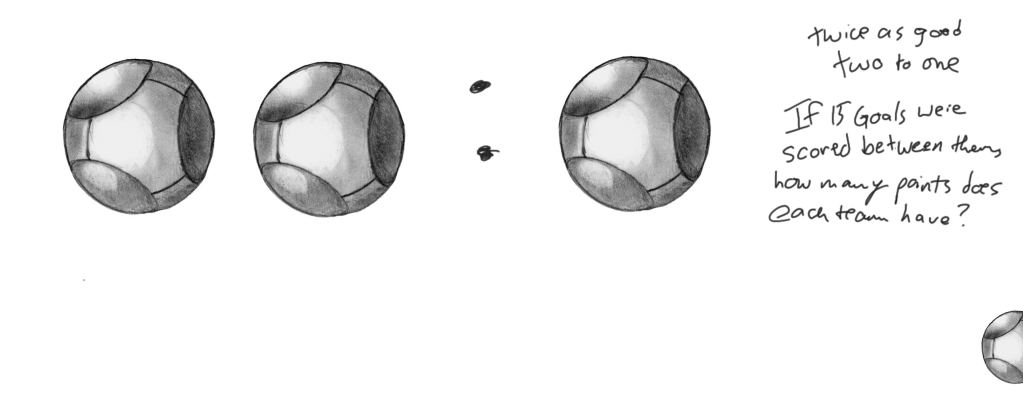
My students deduced we needed one more score for Team A to have more points than Team B. I told the class that Team B, having a ratio of two to one, could very well score one more goal before catching the snitch. “Just to be safe, we ought to say that Team A should score 32 goals to secure victory over a team that catches the Golden Snitch first when working with a ratio of two to one.” 

At this point one of my fourth graders realized that the answer was staring at them from the whiteboard on the other side of the interactive screen on the wall! “Yup,” I conceded. “I worked out this answer with my second graders earlier in the day. We figured it out a different way.” The fourth graders didn’t feel tricked, but just to be sure, I added, “You guys were really fast. It took my second graders and I a while to figure it out.” 

“Now, let’s have some fun with ratios,” I told them, as I wrote “3:1” on the board. “What if Team A was three times as successful at scoring quaffles than Team B, but Team B catches the snitch? Now, how many goals need to be scored by Team A to win?” 

We started off with thirty goals because it is a nice easy multiple of three and close to our previous answer. If Team A scored thirty goals, Team B would have scored only ten. After multiplying both scores by ten and adding the snitch, we found that Team A didn’t have to score that many goals:

30 * 10 > 10 * 10 + 150 With a difference of fifty (300 – 250 = 50), we figured Team A could have not scored a couple of goals and still have won, even if Team B caught the snitch. We tried again. With 27 goals, Team A would have 270 points and Team B would have scored only 9 goals (using the three to one ratio). Nine goals, at ten points a piece, plus the snitch would mean Team B earned 240 points (9 * 10 + 150). This was closer, but can we do better? Does Team A have to score that many points, or could it be less? Sticking with multiples of three, we gave Team A 24 goals. This would mean Team B would score eight. After calculating the math (24 * 10 = 240 and 8 * 10 + 150 = 230) we saw the difference between the two scores shrink to within one goal.

I took the opportunity to point out the consistency in the scores changing. Team A’s score decreased by thirty with each new calculation, while Team B’s score only went down by ten, but every single time. We explored the idea that 30:10 is the same thing as 3:1. I taught the fourth graders that ratios, like fractions, can be simplified by dividing both sides by the same number. “Ratios explain the relationship between two quantities,” I told them. “The smaller the number the easier to understand how they are related. You don’t say 500 to 100. Five to one is just as accurate and easier to understand.”

Just for fun, I gave my group of fourth graders one more scenario; A more realistic one. I told them that the teams were more evenly matched. I made the ratio three to two (3:2). For every three goals Team A scored, Team B scored two. “Using this new ratio, what is the fewest number of goals Team A would have to score in order to win a match against a team that caught the snitch?”

Because we were still working with thirds, the problem was manageable. It didn’t take my students long to figure out that they could work with numbers that were divisible by three, double the third, and multiply both numbers by ten. We took one of our scenarios from the previous problem, 240 for Team A and 80 for Team B, which represented the three to one ratio, and adjusted Team B’s score to represent the new ratio of three to two. I just erased the 80 and wrote the equivalent of two 80s or 160.  

When we found that this new ratio caused Team B to pull away from Team A, students jumped at Team A earning much larger scores. Someone threw out the number 100. I asked them, “What would a third of 100 be?” When no one answered, I restated the question, “What three numbers could be put together to make 100?” Still nothing. I simply told them that it would be 66. I reminded them that a third of one is 0.33. They all sighed with remembrance. They knew that! “When you add some zeros…” I wrote one, and then followed it up with putting a couple zeros behind it. “You move the decimal over. And, since we are talking about a ratio of three to two…” I wrote 66 on the other side of the T chart. After adding 150 for the Golden Snitch, we noticed that the difference was still pretty large.

I showed my students that it was even easier if they began with scores that were divisible by three. From 100 we tried 90. That was simple, but the difference was still too great. Together, we guessed that 81 would be a multiple of three since it is divisible by nine, but how could we figure out the exact number that could go into 81 three times? A tiny bit of long division algorithm did the trick! We did this a couple of times and noticed a pattern. Each time we lowered the dividend by nine, the quotient dropped by three. A really remarkable recognition happened as we figured out the third difference over on our T chart, too. The differences between the two scores were showing signs of a pattern; Each time we shrunk the number of goals that Team A scored by nine, Team B’s final score would drop by exactly 60 points. It went from 810 to 750 to 690 to 630, consecutively! Wow!

The recognition of patterns within the math brought my mind back to what had started this fantastic exploratory math lesson; Stimming. There is something soothing about knowing what number is next. Being able to rely on the consistency of repetition can be comforting. Tapping, singing, pacing, and even skip-counting are all ways to occupy part of the brain, so that other parts may be freed to think. How much stimming a person needs is different for every individual, just like managing it in the classroom environment will differ, but finding just the right ratio can be magical.

Building Strategic Thinking with Dominoes

My 5th grade gifted class revisited the game of Dominoes last week. It took some review, but they enjoyed playing the game. I told them that one of the reasons I had taught them the game was because it is a classic that they could play with grandparents and other elderly people, bridging the gap between generations. The game has been in existence for over 900 years! 

In addition to the game being old, it also presents an opportunity to practice strategic thinking. In an effort to prove this to my 5th graders, I have begun dreaming up scenarios where a player might use analytic skills to make a counter-intuitive move that would benefit them in the long run. 

There are times during a game when you have more than one Bone (Domino) that you can play, but none of the plays will give you points. Sometimes, it does not matter which one you put down, but other times you can plan ahead. Much like you would in chess, you can set up future moves by arranging the Bones to meet your needs. Playing them in a particular order would benefit you more. 

I planned on showing my 5th graders what I meant by setting up scenarios of games and taking pictures. I have done that many times to teach the problem-solving aspect of Dominoes. 

Using photos as teaching tools works great on interactive devices.

Then I thought, Why not have my gifted students make up the puzzles themselves? I will give them the parameters, and they have to try to figure out how to show the need for strategic thinking through constructing an image of a hypothetical game. 

The puzzle would be an image showing Bones (Dominoes) already played, Bones available to a player (standing up so Pips or dots were showing), blank sides of the opponent’s Bones, and maybe a Boneyard (unused Dominoes). 

If you are a novice Dominoes player, some of this vocabulary might be new to you. Bones are the game pieces, named after what they were originally made out of; Ivory or elephant tusks (bones). The Boneyard is made up of the unused Bones lying face down. Face down means that the Pips or dots on the bones are not showing. All you can see is a blank Bone or the uniform design that is printed/carved on every one of the 28 Bones of the set. Bones often have something decorative on the side without Pips, so that players can identify the 0-0 Bone more easily. Every Bone has two numbers on it. There are two ends of the number side of a Bone. No two Bones have the same combination of numbers. Beginning at 0-0, the Bones go up to 6-6. 

The Plan: In order to demonstrate strategies for play, I am going to have my 5th graders come up with puzzles that point to weighted plays. In other words there will be better moves than others. People trying to solve the puzzles will have to analyze the potential moves. Which one is better and why? Puzzle-solvers will be required to explain the move they chose. 

This is from the beginning of the year.

The Work: Arrange Bones as though they had been played in a game. This means matching the ends of Bones; Six is connected to six, three to three, etc. There ought to be four lines of play that a player can connect a Bone to.

Each player has Bones left to play. One set of Bones is standing up, with the number of Pips showing. These are the Bones that the puzzle-solver has to work with. (Normally, when I am teaching Dominoes to students, I have them lay all of the Bones down, so that every student can see all of the Pips. This is so that every single play is a lesson on problem-solving. When one plays a real game, you do not show your Bones to your opponent.)

The Bones that the puzzle-solver has to work with (the ones showing Pips in the image) should have numbers that can be played. They contain the number that is present at the ends of the lines of play. One of the Bones that can be played would cause the sum of all four ends of the lines of play to add up to a multiple of five, which is how one acquires points in Dominoes. This would seem like the best choice to complete the puzzle. 

Because we want this to be a puzzle that causes Domino players to grow in their understanding of the game and not just an illustration modeling how to play, we aren’t going to make the correct answer to our puzzle be an obvious choice. A good head-scratcher will require a player to look beyond the obvious play. 

If four Bones with the same number have already been played, and the puzzle-solver has two of the remaining Bones with that same number, how likely is it that the opponent of the puzzle-solver has any Bones with that number? 

Here is your task: Make it so that playing the Bone that does NOT create a multiple of five is the better play. 

I’ll have to share this lesson with my 4th graders, as well!

How could this happen? If the opponent of the puzzle-solver is forced to draw a Bone from the Boneyard, rather than playing a Bone, not only will they not earn any points, but they will be growing the number of points that the puzzle-solver will get at the end of the round; The round that the puzzle-solver is now more likely to win because they have fewer Bones left than their opponent. 

At the end of each round the player who uses up all of their Bones first gets points from the Pips that are on their opponent’s remaining Bones. In order for the play that did not make a multiple of five in the first place (at the beginning of the puzzle-solving exercise) to be the better play, the final play must provide more points than the potential multiple of five. 

If the multiple of five would have been fifteen, and there is no way, given the Bones that are left, for the puzzle-solver’s opponent to have a total of Pips greater than fifteen (you always round up, so sixteen would go up to twenty), then not playing the multiple of five during play would not necessarily be a winning strategy. Typically, you would play the multiple of five, get the points, and hope for the best. This exercise is designed to show my 5th graders that if you plan ahead, the delay of point acquisition could very well bring a windfall of greater point tallies. Not only is this a good life lesson, but it can help them play the game better in the future. 

Now, if you want to try to figure out how to create a puzzle that fulfills these requirements on your own, without any help, go for it. You can return to this writing when/if you get stuck and need some guidance. The next section provides some helpful hints. 

If you aren’t sure where to start, or you have hit a mental block, check out these ideas.

Some Helpful Hints: 

Limit the available Bones. You can do this several different ways. One is to only give the puzzle-solver two bones to choose from. 

Another way to limit the potential outcomes is to make the lines of play long. Have most of the Bones from the set showing in the lines of play, so that the potential Bones of the opponent is narrowed to only a few possible numbers. The puzzle-solver can reverse-engineer the game to figure out what Bones are left to be played. It’s like “card-counting,” but legal;)

A very effective strategy for creating a doable puzzle is to limit the numbers in play. Idea: Make the ends of the line of play all the same number, and the puzzle-solver has the remaining Bones that contain that number. For example, there is a one at the end of all four lines of play. There are only seven Bones that have a one in them. If four of these are played, and the puzzle-solver has the remaining three, then the opponent cannot possibly play any of their Bones. 

But, the puzzle has the puzzle-solver making the next play. How can the puzzle-solver cause their opponent to have to draw from the Boneyard? See if you can figure it out.

There are a couple of ways to solve this problem. One answer is to provide the puzzle-solver with a double. A double has the same number on both sides. When this is played at the end of a line of play, it keeps that number going! 

Another solution requires more work, and could therefore be trickier for the puzzle-solver to find. Make it so that all of the Bones that the puzzle-solver possesses have numbers on them that can’t be played. You have to position every bone that has any of the other numbers on them within the lines of play. No need to worry about your puzzle-solver using up their Bones because every one of theirs contains the same number as the ends of the lines of play. 

Stack the Pips. Create lines of play that have low numbers, thus ensuring that the Bones that the opponent possesses are more likely to have higher Pip counts. In this way, even if the puzzle-solver would make a fifteen or twenty with the false-solution-Bone (the one that would make a multiple of five and seems to be the better choice for the puzzle-solver to choose), the total Pips that the opponent would have must be greater than the multiple of five. This number work is truly statistical thinking. Out of all of the Bones still available, how likely is it for the opponent to have a high enough number of Pips for the counterintuitive play to benefit the puzzle-solver more? 

This puzzle would allow for the opponent to make a play or two before the puzzle-solver is out of Bones. My student would have to work through all of the possible outcomes to ensure that the puzzle-solver would come out on top. 

3rd graders learn to play Dominoes

Try it out, and make the puzzle fool-proof. When making the puzzle, turn all of the Bones over so that the Pips are showing. Create a model of lines of play. Give the puzzle-solver the Bones they will work with. Now, look at the Bones that the opponent could have. Adjust the lines of play, so that there is no possible way for the opponent to have a way of winning. You also have to double-check that there are only Bones that would cause the opponent to have more Pips than the false-solution. Then turn over the Bones that form the Boneyard, and stand up a couple that represent the unknown opponent’s Bones. 

Conclusion:

Normally, I will do a lesson like this, and then write a blog about it. This is different. I have used my writing to think through what I want to have my 5th graders do. 

My aim is to have them build their understanding of the game of Dominoes and learn statistical analysis through the process of constructing their own puzzles, rather than just solving mine. Hopefully it will be successful, and I can write a follow up blog about how wonderful it went… or the lessons I learned through its execution, pun intended;) 

If you try this idea or one like it, please share your results. I’d love to learn feedback and improve future teaching. 

Sources:

Marcus, M. (2020). How to Play Dominoes . Cool Math Games. https://www.coolmathgames.com/blog/how-to-play-dominoes

Out-of-the-Box Thinking w/ Dominoes

This is a screenshot of the last paragraph + picture from my last blog, with the question of the day above it. I presented this on our Google Jamboard at the beginning of gifted teaching time for students to wrestle with.

I’m back with some more Dominoes word problem work. At the end of my last blog about Dominoes I dreamed up what I thought would be a good problem to get students thinking. It seemed not only doable to me, but I worried that it might be too easy. Not so.

I asked my students, “What is the highest score possible in one play of Dominoes?” I put 28 bones (one whole set) on each table, and encouraged students to move them around looking for the best combination.

This is a screenshot of photos that I used to show students how to connect Bones, adding up all of the ends, and analyzing which Bone would make the best play.

A game of Dominoes proceeds until one player or team acquires 150 points. It takes several rounds to accumulate that many points. During each round the players add Bones (Domino pieces or tiles) to an existing cross of Bones. You have to connect the same numbers, so a 6-4 Bone could not be added to a 5-1 Bone. It could be added to a 4-4 or a 6-6 Bone. When you connect a new Bone to the Line of Play, you add the last number from each end. Your goal is to have a sum that is a multiple of five. Only multiples of five get recorded as points, pushing you closer to the goal of 150; victory.

The first group that I met with are 5th graders. They are still learning the game. I thought that providing the question of figuring out the very best play would create a goal; “This is what I can aim for.” Instead, my students began building towers with the bones and grumbled, “Why don’t we just play Math 24?” Upon self-reflection, I now realize that my word problem was like asking someone who is just beginning to learn how to construct an airplane to calculate how fast it will go. “Dude, let me get the wings on this thing, already!” Ha, ha. Sorry, students.

Before wasting too much time, fostering further frustration, I decided to scrap the 5th graders’ warm up and move on. I made a mental note on the idea of a Math 24 preference, though. This gave me much to think about; More to come on that, soon.

My 4th graders were at their wits’ end.

I didn’t even try the problem with my 2nd graders, who are also novice Domino players. I thought I’d wait and see how my experienced 4th graders, the students whom I taught to play the game last year, would do. These guys would love the challenge, and should have all of the conceptual tools necessary to tackle this problem. They’re the ones in the picture on the Google Jamboard, for crying out loud!

My 4th graders jumped into “Problem-Solving” mode right away. Their biggest hangup was trying to play the game from the beginning. They kept trying to build the arms from the center of the game, forming a cross they way they always do. That won’t work when attempting to find the highest possible score, though. They would have already used the Bones with the greatest number of Pips (that is the technical term for the dots on the Dominoes) on them. Those need to be saved for the ends.

Finally, success!
Frustration.
Start over, and over, and over, again.

I must have told them to, “Focus on the ends of all four arms. Don’t play a whole game. You don’t need the center of the cross in order to calculate the largest point accumulation possible,” a dozen times. I began to feel like a broken record.

This is a picture of the notes from my journal that led to this “Wonderful Word Problem.” I only focused on the ends of the Line of Play. I’d hoped that this is what my gifted students would do.

Finally, I stopped them and taught them a new vocabulary word: Hypothetical. “This is a hypothetical situation. If you could have the ideal play; The absolute best play ever, what would it be? Don’t worry about what was already played. What Bones would give you the very highest points?”

This is truly Out-of-the-Box Thinking. I wanted my gifted students to leave the box of the game and imagine only the very last play. All previous plays are fog. They don’t matter. You can only see the tips of the Lines of Play, and they have huge Bones… Doubles, every one of them; The highest Doubles, even! Eventually, I had to just tell them the answer.

I had one last group to try out my wonderful word problem. I started the Domino difficulty by sharing with my 3rd graders that the 4th graders could not do this. That got their competitive juices flowing! Next, I did not allow them to put any Bones in the center of the cross. “We are NOT playing Dominoes,” I explained. We are figuring out a hypothetical question: “What if you had an opportunity to make a play that gave you an enormous amount of points? How many points would be the greatest possible in one play of Dominoes?”

Believe it or not, the 5-5 Bone is worth more than the 6-5 Bone, because it can be played differently.

I guided their thinking toward the Bones that represent the greatest numbers. Even though a 6-5 Bone has more Pips than a 5-5 Bone, it does not present the greatest value when played at the end of a line. Why? Because, you don’t add the 5 and the 6 from the 5-6 Bone. Only one of the numbers would be available for adding. However, if you played the 5-5 Bone sideways, you’d have ten. Gasps, sighs, intake of breaths… Doubles were explored. I forced them to put the Doubles at the ends of the lines of tape I’d stuck on the tables to guide Lines of Play.

“Place the Doubles at the ends of Lines of Play.”
Afterward, we explored what Bones may have been played previously, working backward from our hypothetical best play.

Letting the 3rd graders figure out answers to my guiding questions, I led them through Out-of-the-Box Thinking. In the end, they felt like they had solved the problem, and they had (with a little guidance from their teacher). Lesson: People can be taught to Think Outside of the Box. It is not necessarily natural.

Candy-Coded Morse Mondays

These two were so excited about earning their treasure through decoding the Morse Coded Monday Message that they just had to take photos of their discovery; a pile of Hawk Tickets in the vacant locker.

Yesterday was Monday, and among other things, that means Morse Code Morning Work for the Polite Pirates! Each Monday, since I introduced Morse code to the class back in January (Coding Teamwork), I’ve provided dots and dashes for deciphering. The prize for first decoder varies. At times it’s an intrinsic reward. One time, I hid a pile of behavior-plan tickets in the locker of a student who never showed up at the beginning of the year. Many of the codes contain riddles, so they are codes within codes.

The riddle within a riddle on this occasion was the vocabulary word “nonexistent” that described the Polite Pirate who had never shown up.

This was the case yesterday. I made up a word problem involving kids and candy. We have been learning fractions, and I was planning on introducing equivalent fractions first thing. Instead of saying, “Today we are going to learn about equivalent fractions,” I buried the treasure within the Morse coded message.  

Admittedly, not everyone was super into decoding this message. When I am coming up with a message, I try to keep it short. I don’t want the task to seem daunting. Another thing I have to look out for is only including letters. I avoid punctuation, and any numbers need to be spelled out. There is Morse code for letters and punctuation, but the image of the coded alphabet that I provide for the Polite Pirates does not have that code in it. (A fun, albeit challenging, task could be having the Polite Pirates figure out the code for numbers by embedding dash/dot combinations into messages that would only make sense after doing some calculating to figure out the answers to math problems. My students could build their own decoder of numbers through doing math, mixed in with Morse code.)

This is a screenshot of what I put into the Morse code translator website.

I messed up yesterday’s code. I accidentally included a number that wasn’t spelled out. When some students came to the “2” within the text, they knew it was a number. Rather than have them figure out what number it was from the problem, I told them it was an upside down five. (I can’t help myself!) It took them less than a minute to understand it was a two. 

Before stumbling across the number within the code, the Polite Pirates had figured out that it was going to be a word problem. This had some of them annoyed and others intrigued. In order to sweeten the deal, I had hinted that there would be a prize for whoever solved the problem first. Of course my hint was also a riddle: “The first to solve this will literally get the answer.” This worked because some of the first few words include “six candies.” My pirates, polite or otherwise, were going to bite onto this extrinsic motivation! Also, I was able to reteach the vocabulary literal versus figurative while they worked. 

When the word “fraction” was decoded, students knew what they were up against. Mr. Weimann was up to his many tricks. This was going to be “fun learning.” We have been working on fractions. The decoding heated up, and students began working in a frenzy. They were ready for this. 

As the final letters and words were discovered a veil of secrecy seemed to lower over the classroom. In order to earn the answer, you must figure it out. Now, students were back at their desks, hunched over their notebooks. “What is the problem about?” I prompted, half for the students working out the word problem, and half for those who were still decoding the Morse code message. I wanted the first half to understand the message of the problem, and I hoped to light a fire under the ones struggling with dots and dashes. This second goal worked, because one of my students who regularly succeeds in decoding these messages first had come into the classroom late that morning. Her pencil nearly carved the letters into her paper as she frantically discovered each letter of code. 

“Candy!” nearly everyone exclaimed, for the rumor had flown around the room like flu germs in a cramped elevator. 

Approaching the students working out the math, I asked, “What are you asked to find?” This is the second of our four word problem prompts that we use as a mantra when performing problem-solving math. 

  1. What is this problem about?
  2. What are you asked to find?
  3. What is the important information?
  4. What are you going to do? (What operations are necessary?)

I informed the front-runners that there was a riddle within the problem within the code. “Don’t be fooled,” I warned. “Look closely at who is getting candy in the end. It is written in the second person,” I instruct. I was hinting at the fact that, while you are sharing the candies with your friends, you still get to have some! “The problem states, ‘What fraction of the candy would each of you get?’” I quietly read to the students who are working out the math. 

One of the students got it. “There are three people and six candies,” he whispers. 

“Mm hmm,” I encouraged.

“Is this it?” His competition showed me her paper. She has not only written the correct answer, 2/6, but she drew pictures to show her work! I tell her yes, just as the boy shows me his paper. He has the same fraction. I then tell them to see if they can “simplify that fraction. Is there any way to make those numbers smaller, but have it describe the same amount of the candy?” They crunch the numbers simultaneously. 

I was so impressed with their work that I took pictures to project on the board.

“One-third!” they exclaim in unison. If I don’t say that they are correct verbally, my face assures them of victory. And, the action of getting a big bag of candy out of a cabinet is more proof of triumph than the class can handle. Everyone’s attention is on the Monday Morse code math masters who have earned the prize; literally the answer to the problem; six candies each to share between themselves and two of their friends. 

Before giving them the candies, I had them explain their work. They took turns writing and drawing on the board, talking their Polite Pirate peers through what they had done. The student who had drawn pictures in her notebook, not only drew them on the board but wrote complete sentences describing the whole procedure. I was so impressed that I was tempted to give her additional candies, but no, I am a pirate captain, if nothing else, and I be stingy with me treasure! (Really, I like to keep my word, strictly, when I can, because I stretch my meanings all of the time!!)

Who to share their treasure with, these two could not decide. I suggested that they witness who goes back to their desk the quietest and does the best job copying what is on the board into their spiral notebooks. The Polite Pirate pair nodded and the race was on… again. This time, every pirate but two were scrambling to get to their seats, sit up straight, and quickly copy everything the first two had explained. The candy captains walked around inspecting the work of their peers. Candy was dispersed, but you couldn’t tell because everyone was feverishly writing. 

And, this is how we began discussing equivalent fractions. As kids crunched on candy, I used the idea of candy to suggest each piece being cut in half or thirds. Halves would produce 4 pieces out of a total of 12 going to each student. Thirds would make it so that 6 pieces out of 18 would be had by each friend. We went backward, too. “How many sixes are in 18?” I asked. I had a worksheet for students to try out, and I circulated my ship… I mean classroom, and checked for understanding. 

One last thing about Morse Code. Some students complained and grumbled about the work of decoding the message. When the dust settled, I told my Polite Pirates that my intention is for them to know the code so well that they do not need to keep referencing the alphabet decoder. I had them try it out. I told them to close their eyes. “What letter is four dots?” I asked the group.

“H!” they called out in unison. 

“And, what letter is only one dot?”

“S,” the class provided. I did this with several more letters that we have seen over and over, and they had used to decipher the message still in front of them on the Monday Morning Board. They were amazed at their memory. I told them that this is how you memorize something. You have to work at it, practice it, use it. I’m planning on helping them memorize the code and see if they can decipher something without me providing the alphabet. 

Building Bridges: A Hands-On Math Lesson

This blog serves two purposes: First, I just shared a lesson with the Polite Pirates (my class) that went so well that I want to share it with everyone. And, second, due to its complexity, several students need additional clarification. I am hoping that by writing this down, I can make clear how the business of bridge-building works.

Yesterday morning I dug out the colorful, connectable, plastic blocks I’d stored away in a bin under the counter. I told my students that they would be building bridges. Cheers rang out. They were to work as a team to construct a way for a car to travel from one pile of dictionaries to another. The Polite Pirates cheered with joy.

“There’s a catch, however. You have to buy the blocks!” I exclaimed. The class groaned. “Each one costs ¼ of a dollar. (I’ve been teaching fractions and mixed numbers.)”

“How much is that?!” a few students grumbled.

“You know how much a quarter of a dollar is,” I accused. 

“Twenty-five cents?” a student clarified.

“Yes. You will work as a team of engineers. Use your Spiral Notebooks to keep track of the number of blocks. You’ll need to figure out the total cost of your bridge.

“Oh, one more thing: Your bridge is going to make you money. That’s right! Sure, it will cost you to build it, but once it is done, you can charge a toll for cars to use it. For every foot of bridge you are allowed to charge one dollar. 

Making money got their attention;)

This is the slightly confusing part (one of them, anyway): If about twenty vehicles travel across your bridge per hour, how long will it take to make (dramatic pause) one thousand dollars? 

Before setting them loose, I showed them that this problem was doable. (The looks on their faces were incredulous.) “Let’s say you build a 10 foot bridge. How much money can you charge to cross it?”

“Ten dollars.”

“Right, but that is $10 per car. If twenty cars travel across your bridge in one hour, how much money do you earn?”

Thinking… “Two hundred dollars,” a student offers. 

“Good; You are correct. Where did that number come from?” I prompt. I want the class to know how to do these calculations.

“I multiplied ten by twenty.”

“Right. If your bridge makes $200 every hour, how long will it take to get to a thousand dollars?” Their minds were working, now! 

“Five!” several students shouted in unison. 

“Don’t forget that you need to use some of that money to pay for the building blocks that you used to construct the bridge,” I remind them. And, they’re off! 

The Polite Pirates had a blast working together. I was impressed that they almost instantly formed the idea of making supports to hold up longer sections of bridge. In this way they could earn more toll money. Of course, they had to count the blocks that they used to hold up their bridge when tallying up the cost of building materials. I didn’t let them use anything other than the building blocks for construction. 

Once the bridges got to be several feet long, every single student on the team was needed to hold the bridge in place as more supports and lengths were added. I overheard one third grader explaining to his partners that even though it would cost more to use extra blocks, they would make more money from tolls, because they could make their bridge longer. I reinforced this idea by sharing, “Sometimes you have to spend money to make money, folks!”

After a timer I had set went off, I had everyone stop building and count up the number of blocks that they had used. One team split up the task by divvying up the sections to be counted. They then added all the numbers together. Next, it was time to calculate the cost of all of those blocks. One team had used 355 blocks! How could they figure out 25￠ per block? 

I reminded them that they already knew what a quarter of 100 was. “Separate the 300 from the 55,” I told them. “Each 100 would be how much?”

“Twenty-five dollars,” someone answered. 

“That’s right. Now, how many twenty-fives do you have? We’re talking about 300 blocks.” I wrote 100÷4=25 on the board. When someone suggested that they needed 3 twenty-fives, I put X3 under the 25. “These might seem like really big numbers, but you already know what ‘three-quarters of a dollar is,” I prompt.

“Seventy-five cents!” a few blurt out. 

“Not cents, though…” I can see the gears turning behind my students’ eyes. It feels like I can hear the steam coming from their ears. They even gasp with understanding. 

“Seventy-five dollars.”

“Now, for the 55 other blocks. Is there a number close to 55 that is divisible by four,” sounded like Greek to them. I reworded my question in a more leading way. “Can 48 be evenly divided by 4?” This connected with their math facts. A student raised his hand.

After deciding that 48 blocks would cost $12, we tackled the leftovers. “What’s left?” I asked the Polite Pirates who were sitting so patiently on the carpet in the front of my classroom. Counting up from 48 to 55, we discovered there were seven blocks left. “How can we figure out the cost of these?”  

When this question was met with blank stares, I quickly drew seven (very ugly) squares on the dry erase board. I drew a hasty circle around the first four. “Each of these cost 25￠. How much money is four quarters?” Lights blinked on in every students’ eyes. 

“One dollar…!”

 “And…” I prompted for the cost of the remaining three unaccounted for blocks. 

“A dollar and 75￠,” a student finished the thought.  

“So, these seven cost $1.75, the 48 blocks cost $12, and the 300 blocks cost $25 X 3,” I summed up our calculations thus far. “What will this team need to do next? Tell the person next to you.” Then I sent everyone back to their seats to work out the costs of their bridges. I told them to figure out the prices independently. Then compare your work with your teammates. In this way you can double-check your math accuracy. 

I walked around the room, helping students with their division facts. There was a wonderful hum of productive struggle. Some individuals figured out that they would have to add more than one additional hour on to their original answer in order to account for the cost of the bridge. Most found that only one hour would do the trick. 

Now that all of the math was done, it was time to write about it. I had posted a question in the Polite Pirates’ Google classroom: “How long will it take for your engineering firm to make one thousand dollars?”

They could work with partners and discuss their writing with their team, but each student was responsible for producing their own explanation of what they did. I left the math that I’d shown them on the board, so they could copy it into their notes, or just write about what we figured out together. 

One of the things I like most about using Google classroom on iPads is how easy it is to use the “Speak to Text” feature. It’s true, you have to teach and practice rereading and editing your text, in order for students to use this effectively, but it speeds up typing entire paragraphs. It also helps facilitate a more “Discourse” -style text. When my students purely type, they are less likely to include opening statements, and they will leave out key details. Through the process of “Telling” their iPads what they did, you get a more structured description. And, because it is easy and fast to do, students don’t have a problem including more details. 

Here are just a few samples of the amazing answers that the Polite Pirates typed into their Google classroom assignment.

I hope you enjoyed hearing/reading about this lesson that my students experienced this week. If you have ideas on ways to improve or modify it, let me know in the comments. Thanks, and take care.

“How to Teach Cribbage to Kids, AND Why They Need to Learn”

(Part 1 of obviously more than 1, but not sure how many just yet;)

With the winter holidays approaching, I wanted to prepare The Polite Pirates (my students) for being stuck in the house with “nothing to do.” While I’m not against video games, I think it’s wise to have some alternatives. 

Hands-on games that promote thinking and problem solving are my favorite to teach and play. Chess and Dominoes are begun early on in the year. Now, it’s time to break out the Cribbage board. 

The fact that there are tiny pieces that could easily get lost makes the unpackaging mysterious and exciting. The board looks interesting, and young students can’t wait to get their little fingers on those tiny pegs! This affords a concrete reward for paying close attention and practicing the game well. 

Teaching Cribbage to children requires a scaffolding approach. There are many rules and ways to acquire points. They must learn all of these before earning the privilege of placing pegs on the board. This motivation helps keep them interested and focused. 

Analyzing combinations to find potential points.

After showing and modeling the board just enough to wet their appetite, I explain that the first part of the game is all about analyzing your cards. You must decide which cards to keep and which ones to discard (They go in what is called a “Crib,” but we don’t worry about that at first). First, I model, looking closely at 6 cards. Leaving out the idea of runs, I explain that we are looking for pairs and combinations that make 15. With only these 2 criteria, we work on adding up card values and counting potential points.

Cribbage for Homework!

[A couple of things to keep in mind: Aces are always valued at 1 in Cribbage, and face cards are all 10. Also, and this is fun for teaching the point system/using combinations, three-of-a-kind is 3 separate pairs, totaling 6 points (2 points per pair).]

Shuffling between rounds makes it feel more like a card game than math practice.

After modeling making wise decisions regarding which card combinations make the most points, I have students try. In groups of 3, I give kids 6 cards to puzzle over. I always shuffle the deck between every “round.” This makes it feel more like a card game and less like math practice.

If interest wanes at all, you could move the pegs on the board. That will get kids into looking for as many points as possible. Also, you could suggest that if one team sees points in another team’s cards that were not discovered and therefore not counted, the team that discovered the missing points gets them! 

In other words, you have Team A and Team B. Each team gets 6 cards. If Team A only found ways to earn 4 points, but when they show their combinations, a player from Team B notices an additional way to make a combination of 15 that Team A failed to see or mention, the sly individual from Team B who uncovered the extra points gets them for their team (B, not A). This keeps everyone on the alert. 

Listen to the amazing thinking going on.

Notice that the students have to use “math discourse” to share what their cards provide. They do this to prove that they deserve the points they are claiming. It allows every player to perform backup mental math. 

This exercise of looking for combinations of 15 will continue in this way for a week or two. Once students have grasped all of the ins and outs, you can introduce “The Starter.” This card is pulled from the middle of the deck after the cards have been dealt. It is placed face up on top of the pile of leftover cards. Students now have one more card to consider when choosing the 4 cards that they will keep. The Starter is static, staying on top of the deck and being used by all teams. 

If you are interested in enriching the decision making process, tell the students that one team will actually get the cards that you discard. The two cards that each team gets rid of go into a “Crib” that the dealer uses to make points at the end of each round. This means that, in addition to trying to figure out what combinations of cards will afford you the most points, you want to keep points out of the hands of others. Don’t gift the dealer with good combinations. Or, if you are the dealer, you can feel comfortable placing a pair or good combination into the Crib. 

Students practice skip counting by twos.

A way to differentiate for your students who are continuing to make progress but could use some help is providing a chart of addends that form 15. You could also have manipulatives or base-ten boards/charts for students to make 15. Make a lesson of looking for tens and fives in number combinations. 

Just as I would have The Polite Pirates practice for a while before introducing further ideas, I will end this blog right here. Playing with numbers, considering the value of combinations, analyzing which cards should stay and which ones should go, students will enjoy the randomness of shuffled hands. “Cribbage affords players both the anticipation of the luck of the deal as well as ample opportunity to exercise their skills in discarding and play” (Bicycle blog).

Card Games Can Be Controversially Classy
Previous blog about Cribbage
https://bicyclecards.com/how-to-play/cribbage/