Decorating the Classroom with Math Enrichment: 5th Grade Word Problem Work

This is my journal entry when I first came up with the idea.

Math enrichment, fifth grade style…

This idea came to me several weeks ago, but I hadn’t had a chance to throw it to my fifth grade gifted students until today. The topic that I started with was volume. The fifth graders were learning the algorithm to solve for volume at the time.

I wanted  to come up with a reason they would need to discover the dimensions of a 3-dimensional space. My background as a painting contractor came in handy. When I estimated the prices for painting ceilings and walls of rooms, I had to do tons of math. How could I bring that experience into the classroom?

I had the idea of working backwards. I would give them a large number, and they would have to figure out the dimensions of the space. 

I decided to turn my fifth grade gifted students into interior decorators. They would need to figure out the measurements of floor space and wall surfaces. 

In creating my math problem I tried out a variety of numbers, multiplying length times width times height, until it created a nice round number. I made the ceiling 8 feet high, and the room 13 by 15. That comes to 1560 cubic feet. Before settling on this number, I tried breaking it up various ways. You could do 12 X 10 X 13 for a higher ceiling. This was good, because I wanted there to be more than one correct answer. 

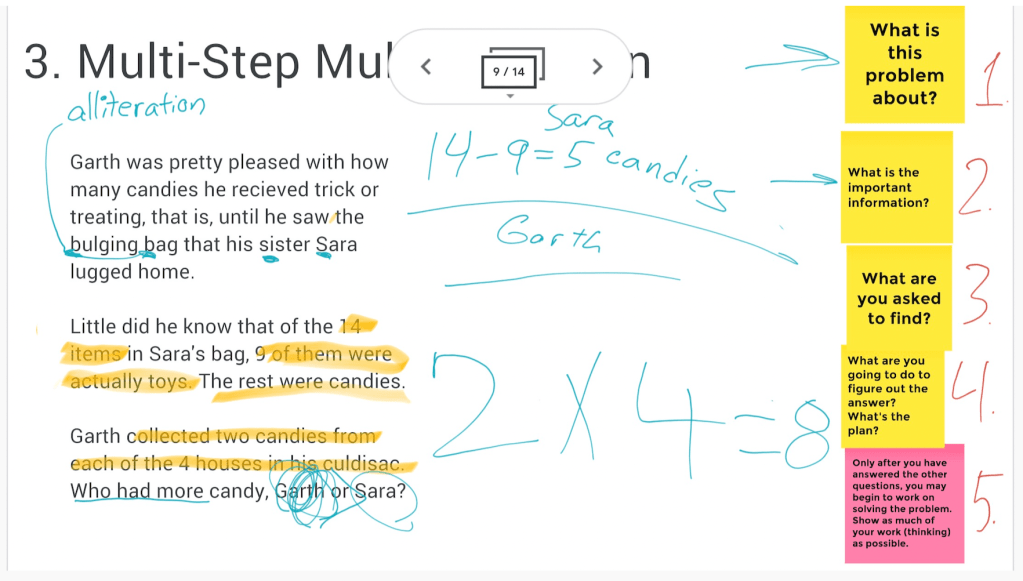
I wrote the problem out and put it on the board for fifth graders to read prior to class beginning. After the announcements, I read the problem aloud to everyone. We practiced our Ready Math routine, the same four-step method I wrote about in a blog about 2nd graders writing their own word problems. First, I asked the fifth graders what the problem was about. Then we discussed what we were asked to find. Next, we identified the information necessary for solving the problem. As it turns out, the only number is 1560, but what does this number represent? And, don’t you know an algorithm that can help you interpret this number? “Yes!” 

I wrote L X W X H = 1560 on the board, when the fifth graders said it. “So, we identified the topic of the word problem; We know what we have to find; What are you going to do with this number and algorithm?” I guided my fifth graders. “You could try making some predictions. Plug in numbers and see what you come up with,” I suggested when I saw that they needed a nudge. 

Some students were still stuck, so I asked them what they thought the space looked like. “A cube,” someone suggested aloud. Dylan jumped on deciding the room was not a cube. He used his iPad to find the cubed root of 1560 to be 11.5977, and since one of the parameters was that the dimensions are whole numbers, this option was off the table. 

“You can’t use your iPad,” a peer protested. 

“I never said anything about not being able to use iPads or calculators,” I offered. Fingers feverishly fought to open devices. Not everyone, though. There were some students who chose to stick with paper and pencil. 

A group of girls asked to use some rulers. When I asked why, they told me that they wanted to get some ideas. This seemed perfect to me. They realized that they needed some background knowledge. They began measuring the classroom. 

A student came to me with the dimensions 40 X 39 = 1560. At this point I brought eveyone together for a teaching moment. “If the room were 40 feet by 39 feet, and the volume of the three-dimensional space were 1560 cubic feet, how high would the ceiling be?” They thought about it for a second. Some multiplied 39 times 40 and discovered that it equals 1560. “The ceiling would only be one foot from the floor! Two measurements would make it a two dimensional space. You need a third measurement to give it depth,” I explain. “What could you do with these numbers?” 

“2 X 20 X 39,” several students say at the same time. 

“So, now we have a two foot high room. This needs to be a space that normal adult humans can walk around and live in.” 

“4 X 10 X 39”

“We are getting closer. Why don’t you do to the 39 what you were doing to the 40? Try breaking it up.” 

After a while, a few students were beginning to figure out more reasonable dimensions for a living space. They thought that they were done when they came up with three numbers whose product produced 1560, but “Oh, no! You still have to do the interior decorating work. Now that you know the lengths and widths of the walls, you must figure out how much hardwood flooring you need to get. And then, you have to calculate how many double-rolls of wallpaper to order,” I remind them. 

I shared the word problem with the class via a Jamboard, so that they could share their work. They could write right on the Jamboard, or take a picture of their papers, using Jamboard. The classroom was electric with mathematicians calculating, communicating, collaborating. I don’t know about interior decorating, but these students were making my room look and sound great! 

Creating Word Problems: Math Enrichment

It’s October, and the second graders in my school are learning the basics of solving word problems. The arithmetic is super simple single-digit algorithms. Likewise, the stories couching the numbers are unadorned with character development, setting, or plot. Time for some #MathEnrichment!

My idea was for the 2nd grade gifted students to write their own word problems. Before creating our own, I thought I’d model some. I wanted to provide some math that was challenging, but doable, albeit with my help. As it turns out, my math riddles had the second graders perplexed to the point of paralysis.

It wasn’t just the numbers. Somehow, I’d forgotten what Ready Math had taught me! There is a specific way to read word problems. Even the smartest of the smart; kids who can wrestle with and make sense of the math; won’t be able to decipher what is being asked of them if they aren’t taught how to comprehend what is going on in a math story. It is like an Olympic runner being dropped into the middle of a forest and expected to sprint to the finish line that she can’t even see.

I constantly tell my students that challenges are fun. These kiddos weren’t buying it. Challenges are only fun when there is some hope.

Like an idiot, I dragged my students through my word problems, doggedly showing them what the numbers were doing. They were good sports. When I let them write on the Google Jamboard, they perked up. In the end, they left my room with number hurricanes storming their cerebrals. I was left to pick up the mess of math misconceptions strewn about the streets of seeming failure.

That was last Friday. Over the weekend I remembered; There is more to solving a word problem than crunching numbers! The Ready Math curriculum instructs teachers to have the students use a 4 step approach to solving word problems. When you break the process down this way, it is much more manageable.

  1. First, read through the word problem and decipher what the story is about. Don’t worry about the numbers. What is the topic? Are we talking about reading books or alien monsters that can control your actions with their minds?
  2. Next, identify the important information. What are the tools you’ll need to fix this problem? Don’t be fooled into thinking that unnecessary numbers or information will be needed. Sometimes there are superfluous facts stirred into tricky math stories to trip you up!
  3. Before doing any math, you must figure out what you are asked to find. (This step might come second. I can picture needing to know the end goal prior to identifying the important info.)
  4. Finally, we begin doing some math. Show all of your work/thinking.

There’s a fifth or bonus step that I told my 2nd grade gifted students about, that has to do with communication. Just like we include publishing in the “Writing Process” and the “Scientific Method,” we are not done solving our word problem until we share the answer. Make sure to label the numbers with whatever unit of measurement or name of thing you are talking about!

The answer of this word problem doesn’t even have any numbers in it! But, you better show and be prepared to explain your work for full credit.

Tuesday morning, the day after Indigenous People/Columbus Day, we were back at it with more challenging word problems. When I first showed my students this Jamboard, I had the “sticky notes” layered on top of the word problem. As we read and discussed what each one meant, I moved them to the sides and shrunk them, so that they all fit on the right for reference. Only then, did we read this word problem.

My 2nd graders kept yelling out numbers, like there was a contest for who could solve the problem first. It was humorous to tell them that every single number that they would say, no matter what it was, would be wrong. This was perfect for drawing their attention to step 3. “What are you asked to find?”

“Are you supposed to provide a number as an answer?” I asked my students. This got them thinking. And, even after solving how many candies each kid had, they still needed to compare the numbers in order to really finish the problem. It wasn’t enough to just know how many each had.

This is only the first of many word problems to come for our 2nd grade gifted students.

Once we had successfully solved our Trick or Treat word problem, it was time to make up our own. Before getting creative, we decided on the numbers and operation. We would have the mathematicians subtract seven from twenty.

I wanted to include everyone’s ideas. That is why the math story has flowers named after a student’s pet bunny, a main character named “Kid Pineapple, robots, laser blasts, and lots of the word “stinky” in it. Ha ha. We had a figurative blast coming up with our story.

We look forward to making up and writing down many more for our other 2nd grade friends to solve… The Ready Math way.

Box O’ Blocks: Math Enrichment

Looking for a fast math lesson to extend learning and use critical thinking? You’ve come to the right place. Because I only get to see my gifted students for 40 minutes a day; and that includes walking in the door, settling down, packing up, and exiting; I must make my lessons quick. Recently, I built onto a lesson that I loved in the past: “Box O’ Blocks.” 

Prep: Take those classic, little-kid, wooden blocks and stick 3-digit numbers on the sides. Put them in a box. You are ready to go! 

If you don’t have access to blocks, you could draw, color and cut out different shapes on card stock or index cards. Basically, simulate the classic building blocks, but 2 dimensional. Have the kids make them for ownership of the game. (Instead of “Box O’ Blocks,” it could be “Construction Cards.”) This would be easier to store, lend to other classrooms, as well as quieter;)

I began with a game so simple my 3rd graders could learn and play without use of any writing materials. Pull three blocks out of the box. Round them to the nearest hundred. Add them together. Closest to a 1000 wins.

Our first round had two teams get 700 and the third sum was 1300. At first they thought that thirteen hundred won. “Wait a minute,” I warned. “Are you sure?” Upon revisiting the numbers after I wrote them on the board, my students realized it was a tie! 

After a few rounds of this, I introduced the idea of trading a block. “If you could trade a block to make your total closer to a 1000, which one would you eliminate?” They hadn’t seen all of the numbers but enough to make an educated guess. “If you have three blocks, and they are the numbers 513, 522, and 346, you might want to trade the largest. It puts you way over 1000. This would make room for a block closer to 200.” 

Another fun variation that you could try; I didn’t, so I don’t know how well it would work, but it seems fun; is to let teams trade with each other. 

Here’s some easy-to-use enrichment: Rather than round to the nearest hundred, have students round to the nearest ten. Or, you could do what I did in my original lesson; Don’t have them round at all. They will need paper, dry-erase boards, or iPads to write on for this. 

What I did with my gifted students is I had them actually construct towers that they measured to use an additional 3-digit number for lowering or raising the sum of the original three blocks as necessary. Here’s how it worked. Pull three blocks from the Box O’ Blocks. Round to the nearest ten. Add the three numbers. Evaluate how close you are to 1000. The difference is what you want to make up. If you are over a 1000, you want to take away from your sum. If you’re shy of a 1000, add. Next, you get to build! 

Students construct towers with their three blocks. They then use rulers or yardsticks to measure from the base of the structure to its highest point. Round to the nearest inch. Multiply that number by ten, and either add or take it away from your original sum. The trick is that the students can reconfigure the structure to be taller or shorter. 

This lesson incorporates an idea I had several years ago: Action. I wrote a blog all about an elaborate lesson involving purchasing blocks, constructing castles, homes, structures and renting them to make back their initial investment (purchase price). It was fun, but long; Great week-long project. 

Looking at the Jamboard images in Google Classroom makes it super easy to assess.

The way that I assessed the success of each group/student and the lesson was through the use of Google Jamboard. I made a Jamboard with the instructions on the initial board, leaving plenty of blank space. This was pushed out through the Google classroom, “mak(ing) a copy for each student.” I modeled how to use the Jamboard to take pictures of the blocks, showing the numbers. Then I used the writing tools in Jamboard to write the rounded amounts of each block. I added them all together for a total that could be evaluated next to a thousand. We discovered that I was over one thousand, so I will want to subtract. Once we got the blocks to reach the perfect height, where the number of inches times ten would lessen my original number just right, I used Jamboard to take a final picture and show my last computations. 

It is very easy to create a new board by pressing an arrow at the top of the screen. Then you start over. Pull three new blocks…

One group was 380 more than 1000. They were trying to make their tower 38 inches high, so that they could take 38X10 away from 1380. I told them to trade one of their blocks for another from our Box O’ Blocks. When they went to trade a teeny tiny one, I questioned them. “That block is only 300 (It was actually 296). The other two are both over 500. If you traded one of the blocks that was worth a lot, you might not need to construct as tall a structure.” They were interested in trading the tiny block because they were aiming for height, but was that the best strategy? 

I summarized this story to close our class time. And, it was off to collect some more gifted students from a different grade to teach a different lesson. 

Dominoes Versus Math 24; A Debate

A couple of weeks ago I was introducing the game of Dominoes to my 5th grade gifted students when one of them grumbled that they would rather play Math 24. I did not take offense because I understood why he felt that way. This student is good at Math 24. He already knows how to play it. And, the gifted program practiced it a lot last year, so he was used to doing it. Dominoes was new. It seemed overly-simple. Luck is involved, so you are not completely in control of your success.

If you don’t know what Math 24 is, I’ll explain. The typical game (There is more than one version.) involves cards with four numbers on them. You have to use all four numbers in order to create 24. You can use any operation; addition, subtraction, multiplication, and/or division. There are difficult, medium, and (relatively) easy cards. 

The way the game works is a group of students will sit around a table, and a card will be placed in the middle. The first student to find the algebraic expression to create 24 taps the card. If they can describe the process of acquiring 24 from the four numbers, they get to keep that card. 

There are Math 24 competitions. Our school has done very well in the past. Although I plan to allow time to play/practice Math 24, so that we do well again this year, I want my students to experience more. There are other math games in the world.

One of the reasons I like Dominoes is because of how old it is. Created in China around 1300AD, our current Domino game was adapted in Europe, where it received sixes and its name. You see it played all over the place by senior citizens. It is a relatively simple game that involves mental math to add mostly single-digit numbers. There is strategy involved, because you want to get rid of all of your Bones before your opponent. You can find Bones (game pieces) in any game room, recreational or community center, and most toy stores.

When my student complained, I assured him that we would work on Math 24, but I also pointed out some of the game’s weaknesses. I don’t think that these 5th graders were used to this; How could a teacher be in any way negative about a teaching tool? Weren’t they all sacred? “Can you play Math 24 with your grandpa?” I asked.

“We could teach older people how to play…” These students are in the gifted classroom for a reason. I can easily imagine them dragging a box of Math 24 cards around with them and spurring on the elderly of retirement communities to rekindle their number sense.

I really like Math 24. It greases the wheels of the computational side of the brain. When you play it, you look for patterns and relationships between numbers. One must have speedy mental math recall of multiplication and division facts, motivating students to memorize their basic math facts.

I stuck up for the game of Dominoes. “Yes, it may be simple, but you were unable to solve the word problem that I had presented,” I reminded him. This was a big part of why he had grumbled. I don’t think that my gifted students are used to NOT being able to figure things out. As I made my points in favor of learning Dominoes, a couple of students got on board with my thinking. One student jumped out of her chair and came to the front of the room to deliver an impromptu speech about how Dominoes is better than Math 24. As she wrapped up, a Math 24 supporter yelled, “Objection!” He was interested in providing a rebuttal. And, this is when I channeled the energy into a formal debate: Math 24 versus Dominoes. 

I drew a T chart on the board and had students do the same in their gifted journals. We wrote a few pros for each game in the corresponding sides. I told the students to come up with more on their own. “Don’t just write down ideas that support your side,” I warned them. “Imagine what your opponent will argue. This way you can combat their reasoning. You will have to come up with attacks to weaken their position. It will be easier if you can preempt what they might say.” 

With that, they were gone. Back to regular ed, they went, new and exciting plans for the future swirling through their heads. 

I’ve done debates with The Polite Pirates (my 3rd grade students) before. They have gone well, but the one thing that I struggled with is the conclusion. Normally, I curate the debate so that both sides are pretty even. Then, in the end, I declare it a tie;) Everyone whines and complains, but we all go home content. I tell them that both sides won, as well as myself, because, “You all worked so hard and got so much out of the experience.” 

This time, I wanted to try to make the debate a little more formal. If I expected my 5th grade gifted students to work at thinking and planning their arguments, I should do my due diligence and deliver an acceptable format with a point system. I searched online, and found a blog about classroom debates that offered some good tips. 

The morning board the next day told them to take a picture of their journals and import it to the Google Classroom assignment I’d just posted. When I arrived at the doorway, after AM car duty, some students were writing in their journals. Others were following directions and taking pictures. I didn’t let the 5th graders enter the classroom without some kind of photo uploaded to the assignment. They could take a picture of what they’d copied from the board the day before. That was acceptable; Not ideal. I praised students for their effort, not the quality of their content. (This will be the topic of a future blog.)

I quickly went over the schedule for the debate. The times were modified to fit within our abbreviated class time. (I have my gifted students for just 40 minutes.) Then I went over the things that could earn points. After securing nods and thumbs-up signaling everyone was in sync, we had our opening statements. The Dominoes team went first. They had written an opening statement that two girls delivered in front of the class. Wearing cool sunglasses, their theme was that Dominoes presented an opportunity to have fun and practice problem-solving in a casual, low-stress style. 

Next came the Math 24 team. They came prepared with props, images to share via the classroom projector, and excellent points. In addition to some of the basic differences between the two games, the Math 24 team brought up the idea that the Bones of Dominoes can come from literal bones of elephants. Many sets of Dominoes are made out of ivory, which means… “By playing this game you are supporting the killing of elephants.” Gasps were audible.

When Team Math 24 was finished we were scheduled to have a one-minute “Prepare for Rebuttal” time, but there was a lockdown drill. This ate up the last of our time together. I told everyone that, instead of one minute, you have one day.

The day-long break turned into an entire weekend! When I walked up the stairs after finishing car duty Friday morning, the hallway was empty. Fifth grade had gone on a field trip. A couple of girls came to my room later in the afternoon, after everyone had returned, to ask if we could still have the debate. Because I pull students from several classrooms, and I hadn’t spoken with those teachers, I had to say no. “We will debate on Monday,” I told them. “Do more research. Produce strong rebuttals to the arguments that you heard in the openings.”

They were ready on Monday. The first thing that I did was replay the opening statements that I had recorded with my phone. Everyone was glued to the screen, listening for weaknesses. Team Domino got to go first, since their opening statement was first. They focused on the idea of cost. This was one of the points made by Team Math 24, in their opening statement. “There is more than one kind of Math 24 game,” they are argued. “If you want to play with integers and fractions, you have to pay more.” When it comes to ivory Bones, “You don’t have to buy a Domino set that was made out of ivory, and just because some are ivory, doesn’t make the whole game evil!”

When Math 24 came to the front of the room, they were in attack mode. “Dominoes has too many rules, and doesn’t require anything more than simple addition, and a little bit of multiples,” a student suggested with zest. As far as the cost was concerned, he screen-mirrored images of Dominoes and Math 24 sets from the Internet. It seemed to me that the price difference was minimal.

Both teams did an excellent job involving everyone. Different students took turns talking, and they seemed to really listen to one another during planning breaks between sessions.

Some students representing Team Domino got up to refute the monetary attack. They showed more images that made it appear you could get either game for the same price, thereby neutralizing that argument. That seemed smart to me; Like, move along. New topic, please.

No can do. Math 24 people then got up and accused the Domino team of sharing “sale prices.” This was very entertaining for me to sit back and watch. The students were animated and passionate, but they were behaving civil and being respectful. It genuinely seemed like they were enjoying this playful debate about topics that were not life and death. Math 24 ended their time with the idea that someone could accidentally buy a set of ivory dominoes. Okay, possible, but that does not make the game inherently wrong to play.

Finally, it was time for closing statements. The twins tackled delivering the concluding remarks for Team Domino. They mentioned prices, but focused more on the fact that Math 24 is all about computation, speed, and therefore stress. Dominoes is geared toward problem-solving. They pointed out that because the game is common, you are more likely to find it at a friends’ house or game room.

The Math 24 students had what I thought was a thoughtful rebuttal to the attack of stress-inducing play; You could increase the time of the game, relaxing the mood of play. It isn’t impossible to experience a casual, friendly game of number-crunching. Their idea of a box of Math 24 cards having 96 different cards in it, while a Domino set has only 28 bones fell flat, because the computational-quizzing cards can only be used one way; once and done. Whereas Domino games can be played in endless variations.

We had used up nearly every minute of our time together. Before dismissing my 5th graders back to their regular ed classrooms, I praised their inclusivity; teams did a wonderful job of including everyone. I commented on how well-mannered they all were. And, of course, I loved the thoughtful points that were made. “I do have a critique, however,” I warned. They braced for impact. “Everyone got stuck on the price war.” I saw looks of understanding and acceptance on faces. “You kept coming back to how much each game cost, even after someone from Team Dominoes rightly pointed out that they both basically cost the same amount,” I pointed out. “It is easy in a heated debate, when emotions are high, to not think as clearly. That is why I wanted to mention this. As an outside observer, it would have been more powerful to move away from prices and focus on play.”

Thinking back, I wonder if my students focused more on the price of the games because it was the most tangible concept to debate. It came with pictures and concrete proof. You can’t argue that five dollars is more money than ten! This point did not carry any weight, however, because I already own plenty of both games.

This is an image of my journaling prior to ever suggesting the debate. As you can see, I came up with plenty of reasons for playing both games.

More than who won, students wanted to know which math game won. “Which game will we play, Dominoes or Math 24?” they asked me Tuesday morning. We worked on preparing to make videos to share with Columbia University, instead. I wanted to compose this blog before announcing a winner. Little did they know that we’d be playing plenty of both throughout the year!

Paradoxically Powerful Parameters

This student took a picture of himself, so that he had a model for his artwork.

As promised previously (Parameters Are Classy), I can’t help but explore the profound paradox of boundaries liberating thinking. How could a strict rubric extend creativity and help students be even more successful? That seems counter-intuitive. Don’t rules hamper the imagination? Buckle up, because I plan to argue that tightening up the parameters actually helps foster inventiveness and deepen artistic design. 

Several years ago, I did a get-to-know-you lesson where I had my 3rd grade students, The Polite Pirates, make self portraits. It was the beginning of the year, and I thought that this would be a fun way to both decorate the room and learn a little bit about the personalities of my pupils.

The Polite Pirates (politely) stormed the art room and used scrap pieces of construction paper and loads of glue; NO scissors or any drawing tools; to make our self portraits. Each student was supplied with a 12” by 18” piece of construction paper. They were told to tear the scrap papers with their fingers, and glue them onto the large piece of colorful paper. “It should look like you, but it obviously won’t be a photograph,” I told them. “Have fun with it and be creative.”

I had made an example the night before. I showed them how mine had some 3-dimensional qualities; my bowtie was a loop that you could see right through if you turned the artwork, and my hair (I still had a little at the time–this was a while ago;) curled off of the paper. I also pointed out that you don’t have to use realistic colors. I made my hair blue and green. 

You were supposed to include something that made you unique, and it didn’t have to be your looks. For instance, I made my hair blue and green to symbolize the ocean, because I like the beach. I had curled each hair, so that it stuck off of the paper, not just because I had curly hair, but to simulate waves. I also pointed out that I gave my self-portrait-me a bowtie, because that is kind of my thing. I wear bowties every Tuesday (#BowtieTuesday !).

This was a reply to @LeonoraBenton3 on X.

The Polite Pirates tore it up… Literally! They jumped right into the assignment, and we were nearly done in less than an hour. Only a few needed to add a little more detail to their portraits. They came out great and our classroom was adorned with these magnificent portraits for most of the year. 

Skip ahead to this year. As I prepared to teach the kindergarten through fifth grade gifted students at my school, transitioning from solely 3rd grade teacher to gifted teacher, I thought about doing this self-portrait lesson again. Only, this time I didn’t want my students to be so limited. I was curious to see what these bright students would come up with if I took away the strict parameters of having to use only scrap papers, and prohibiting scissors or drawing tools. This time, students could cut, draw, and even bring in items from home to stick on their self-portrait. 

I showed my gifted students and talked about the self portrait project from long ago. I mentioned the parameters of the previous project, but informed this year’s students that the laws were loosened. I thought that this would free them to be more creative and therefore motivated. I was very surprised at what happened next.

Many of my gifted students floundered. Several had no idea where to start. The students who led the charge into artwork did so by following the guidelines of the previous lesson, tearing scrap papers to glue onto their colorful construction paper. I reminded them that they did not have to do this. They could use scissors. They kept right on tearing away. That was the mental framework (imagination-parameters) that I had set up for them. It was like water running downhill through the path of least resistance.  

There were a few rules: The self portrait was to be contained to a 12” by 18” piece of paper. The student had to produce it. No getting parents to do the work for you. And, no printing something out to paste onto the paper. Also, I told them that it had to be done by Friday, but I wanted it to be worked on all the way until Friday. In other words, no drawing something simple on day one, and saying, “I’m done.” 

A couple of students used pencils to draw a picture on their papers. They had to be pushed into continuing to work on their portraits. Some students got stuck looking at pictures or using a drawing app on their iPads. They wanted to print out their digital drawings. I eventually had to tell them to put the electronic tools away and focus on their paper projects. 

This student made a sculpture of herself out of tin foil, covered it with purple table, and placed a handmade book in its hands.

In the end we completed our self portraits by Friday. They all got hung on the wall. Each one is very unique, represents its creator, and fulfills the requirements. Some of them are super creative. I was able to learn a little bit about the students through witnessing how they tackled the project. In that respect the lesson was a success.

I also learned a valuable lesson about parameters. Generally, students do better when the parameters are tight; not rigid; but clearly and firmly established. Not only was my original self portrait project completed quicker, but if I were to conduct a survey, I think that the first lesson produced more positive vibes when it was all said and done. My gifted students were flummoxed with what to do and how to do it. 

When there are strict parameters, every portrait had the same characteristics. Each was made from tearing and gluing paper. There was no flexibility for someone to bring a cool item from home to stick onto their portrait. Even though every portrait was very different, they were equal. 

In order to preempt any unfavorable feelings of comparing someone’s portrait to another’s this time around, I put it right into the rubric. I told all of the gifted students on the first day that this was supposed to be fun, and that there will be no judging. Do your best on your work, admire your neighbor’s work, but do not say anything negative about anyone else’s artwork. If someone chooses to draw a stick figure, they can. It simply has to represent the artist in one way or another, be done by Friday, and be worked on until Friday. Good luck making that last parameter stick with your line art! 

This student kept the outer boundary of the 12X18 construction paper, but attached a box to it so that she would have a stage for her self portrait to pirouette! Out-of-the-box-thinking inside a box.

When I had very strict guidelines during the tearing and gluing lesson years ago, there was still room to be creative. It was more challenging to make your portrait unique since everyone was using the same mediums, but the uniqueness was more evident. The difficulty-level caused students to stretch their minds. Whenever I am given a task in a grad class, at a professional development session, or at a seminar, I always see how far I can bend the rules and still remain within the parameters of the project. This helps me make a boring (sorry teachers of teachers; they are) requirement fun or at least less mind-numbing.

When you narrow a channel of water, it becomes more powerful. Parameters are boundaries. Like a pressure washer, they focus all of the energy and attention on specific goals. 

Experiment: Make a barrel for a projectile to travel through. The parameters are the sides. Shoot something through the barrel. Shoot something with absolutely no parameters. Which goes farther? Which is more accurate? At what point do the sides prohibit the distance? When do the parameters prohibit success?

This student used only different colored tape to make his artwork.
He created his own parameters.
This student used his 3D printer to make a model of his 3D printer. So cool!

Parameters can standardize results. This is often perceived as a negative thing. Educators don’t like being boxed in, confined, or limited. Rubrics guide our evaluation of students’ work. Using one to score a writing piece does not mean that students can’t use narrative to explain a nonfiction topic. It focuses attention on whether the student developed and mastered the skills taught. If you are looking to see if a student can research a topic, and they decide to show you that they can through producing a play, were they wrong? Did you put in your rubric that it has to be a six-sentence-paragraph? And, if so, why? Are you measuring mastery or how well the kid can be squeezed into a box?

I’ll end this parameter perusal on a positive product from my most recent self portrait lesson. Don’t be afraid to be creative in constructing parameters. I told my gifted students that they were not allowed to get stressed out. I put it in my rubric. If they felt like they were getting worried, they had to talk to me. This was supposed to be fun. If it wasn’t fun, they were not doing the assignment correctly. “I will dock points from anyone not having fun,” I mock threatened to smiles. My aim was to introduce my students to my goal; Which is to make working hard and tackling challenges entertaining.

Pull the string to see the student pirouette; Push the button to light up the idea above another pupil; And, check out the shelf our reader is sitting on!

I already mentioned that, in addition to completing the artwork by Friday, they had to continuously work on their projects when they were in class. If they weren’t working, they were not meeting the expectations. This allowed me to praise them for working, rather than on the product of their work. (More on this later.) Lastly, as mentioned previously, rather than only telling my students to not view this project as a competition, I put it right into the rubric! 

Out-of-the-Box Thinking w/ Dominoes

This is a screenshot of the last paragraph + picture from my last blog, with the question of the day above it. I presented this on our Google Jamboard at the beginning of gifted teaching time for students to wrestle with.

I’m back with some more Dominoes word problem work. At the end of my last blog about Dominoes I dreamed up what I thought would be a good problem to get students thinking. It seemed not only doable to me, but I worried that it might be too easy. Not so.

I asked my students, “What is the highest score possible in one play of Dominoes?” I put 28 bones (one whole set) on each table, and encouraged students to move them around looking for the best combination.

This is a screenshot of photos that I used to show students how to connect Bones, adding up all of the ends, and analyzing which Bone would make the best play.

A game of Dominoes proceeds until one player or team acquires 150 points. It takes several rounds to accumulate that many points. During each round the players add Bones (Domino pieces or tiles) to an existing cross of Bones. You have to connect the same numbers, so a 6-4 Bone could not be added to a 5-1 Bone. It could be added to a 4-4 or a 6-6 Bone. When you connect a new Bone to the Line of Play, you add the last number from each end. Your goal is to have a sum that is a multiple of five. Only multiples of five get recorded as points, pushing you closer to the goal of 150; victory.

The first group that I met with are 5th graders. They are still learning the game. I thought that providing the question of figuring out the very best play would create a goal; “This is what I can aim for.” Instead, my students began building towers with the bones and grumbled, “Why don’t we just play Math 24?” Upon self-reflection, I now realize that my word problem was like asking someone who is just beginning to learn how to construct an airplane to calculate how fast it will go. “Dude, let me get the wings on this thing, already!” Ha, ha. Sorry, students.

Before wasting too much time, fostering further frustration, I decided to scrap the 5th graders’ warm up and move on. I made a mental note on the idea of a Math 24 preference, though. This gave me much to think about; More to come on that, soon.

My 4th graders were at their wits’ end.

I didn’t even try the problem with my 2nd graders, who are also novice Domino players. I thought I’d wait and see how my experienced 4th graders, the students whom I taught to play the game last year, would do. These guys would love the challenge, and should have all of the conceptual tools necessary to tackle this problem. They’re the ones in the picture on the Google Jamboard, for crying out loud!

My 4th graders jumped into “Problem-Solving” mode right away. Their biggest hangup was trying to play the game from the beginning. They kept trying to build the arms from the center of the game, forming a cross they way they always do. That won’t work when attempting to find the highest possible score, though. They would have already used the Bones with the greatest number of Pips (that is the technical term for the dots on the Dominoes) on them. Those need to be saved for the ends.

Finally, success!
Frustration.
Start over, and over, and over, again.

I must have told them to, “Focus on the ends of all four arms. Don’t play a whole game. You don’t need the center of the cross in order to calculate the largest point accumulation possible,” a dozen times. I began to feel like a broken record.

This is a picture of the notes from my journal that led to this “Wonderful Word Problem.” I only focused on the ends of the Line of Play. I’d hoped that this is what my gifted students would do.

Finally, I stopped them and taught them a new vocabulary word: Hypothetical. “This is a hypothetical situation. If you could have the ideal play; The absolute best play ever, what would it be? Don’t worry about what was already played. What Bones would give you the very highest points?”

This is truly Out-of-the-Box Thinking. I wanted my gifted students to leave the box of the game and imagine only the very last play. All previous plays are fog. They don’t matter. You can only see the tips of the Lines of Play, and they have huge Bones… Doubles, every one of them; The highest Doubles, even! Eventually, I had to just tell them the answer.

I had one last group to try out my wonderful word problem. I started the Domino difficulty by sharing with my 3rd graders that the 4th graders could not do this. That got their competitive juices flowing! Next, I did not allow them to put any Bones in the center of the cross. “We are NOT playing Dominoes,” I explained. We are figuring out a hypothetical question: “What if you had an opportunity to make a play that gave you an enormous amount of points? How many points would be the greatest possible in one play of Dominoes?”

Believe it or not, the 5-5 Bone is worth more than the 6-5 Bone, because it can be played differently.

I guided their thinking toward the Bones that represent the greatest numbers. Even though a 6-5 Bone has more Pips than a 5-5 Bone, it does not present the greatest value when played at the end of a line. Why? Because, you don’t add the 5 and the 6 from the 5-6 Bone. Only one of the numbers would be available for adding. However, if you played the 5-5 Bone sideways, you’d have ten. Gasps, sighs, intake of breaths… Doubles were explored. I forced them to put the Doubles at the ends of the lines of tape I’d stuck on the tables to guide Lines of Play.

“Place the Doubles at the ends of Lines of Play.”
Afterward, we explored what Bones may have been played previously, working backward from our hypothetical best play.

Letting the 3rd graders figure out answers to my guiding questions, I led them through Out-of-the-Box Thinking. In the end, they felt like they had solved the problem, and they had (with a little guidance from their teacher). Lesson: People can be taught to Think Outside of the Box. It is not necessarily natural.

Dominoes Word Problem: Math Enrichment

I used to use a giant set of Dominoes to introduce the game to The Polite Pirates (my 3rd graders).

Playing the game of Dominoes is an excellent way to introduce and practice problem solving. I’ve used this game for several years in my 3rd grade classroom, and now I am introducing it to my gifted students. 

This past week was the first week that I met with my elementary (K-5) gifted students. Obviously, the various grade levels were in different places when it came to math concepts. Second grade is working with word problems. Third grade will be tackling multiplication soon. Fourth grade is focused on geometry right now. And, 5th grade is preparing to use formulas to solve for volume. 

Dominoes can be used to introduce multiplication, using cumulative property, strengthening mental math, not to mention strategic thinking.

Tuesday morning’s second grade gifted lesson began with my typical introduction to Dominoes. I told the students that each tile is called a “Bone” and the pile of unused tiles is the “Boneyard.” They learned that there are always 28 Bones in a game, and that every single Bone is different. Each one has two numbers on it, even the ones that look empty! “What number is on this side?” I asked holding up a Bone with a six on one side while the opposite was blank. They didn’t skip a beat in guessing “Zero.” 

It took a little longer to explain adding the ends of each Line of Play. “You add up any number that is at the tip of an arm, no matter how long or short the line is,” I told them. We practiced some play. The adding wasn’t a problem. We discussed using the cumulative property to switch up the order of numbers, so that the mental math was easier. “Look for combinations that create ten,” I told them. “Rather than adding 4 + 5 + 4 +2 equals fifteen, combine the 4, 4, 2, first. Then you instantly know that the five makes fifteen.” 

I let students draw and write on the Google Jamboard to show and explain their thinking.

“Points are only awarded when the sum is a multiple of five. The ends of all of the lines of play add up to ten. Is that a multiple of five?” They knew that ten was made up of two fives. “How many fives are in 15? 20? 50? 500?” Flawless computation… Multiplication, here we come!

“Whenever you earn points, you say, ‘Give me ten…’ or however many points you earned.” I learned this from a fun video that taught me how to play ages ago, and elementary students LOVE this aphorism. 

“Give me ten!” one of my second graders beckoned. I put 10 on the board, and we played a couple more sets before moving on to our Self Portrait project. Even though I only have my gifted students for 40 minutes at a time, I found doing more than one mini lesson to be helpful in keeping their interest. 

After school, I came up with a word problem for Wednesday using Dominoes. I typed it into a Jamboard. Even though I tried to word it in such a way that you could visualize the game in your mind, I went ahead and used Domino tiles (Bones;) to make a model of the hypothetical game on a table and took a photo. I imported the picture on the Jamboard slide with the word problem text. 

I snapped this pic, so that I could show my students the thinking behind their word problem. I am hoping to inspire them to use their “Gifted Journals” to jot down ideas through drawing diagrams and writing notes just like this.

When Wednesday arrived I was excited to try out my word problem. The first group of students that I met with was 5th graders. Because I do car duty, I get to my room at the same time as my students. This morning I had placed a note on the open door, instructing them to try to work out the answer to this problem while they waited for me to show up. The word problem was presented on a giant Google Jamboard that I’d rolled in front of the entrance to the room. 

The group was crowded around the screen when I got to my room. I enjoyed listening to their discussion of possible moves. From what I heard, a couple students were aware of the general concept of matching numbers. They didn’t quite understand adding all of the numbers from the end of each line of play, but that was okay.

When one of the students decided the trick to solving the problem was to simply take a new Bone from the Boneyard, I invited the 5th graders into the room. Before talking Dominoes, I praised their persistence and told them that I was proud of how hard they worked. I purposefully pointed out the failure to solve the problem as an example that not everything will come easily to them. It is my job to come up with challenges that stretch their thinking, and I intend to make not only their intellects but also grit grow. 

As I explained the solution to the puzzle, I used it as a teaching tool. When I informed them on how the points work, they noticed that placing the Bone with the two on one side at the end of one of the lines of play would bring the total sum of all of the arms to 20, a multiple of five, and thereby an opportunity to earn points. “Good. But, there is a third and less obvious option,” I told them. “This one,” I said, pointing to the Double that had a six on both sides, “Is a Double. It is special. Not only can you play it with one six touching the line of play (also a six), but you can set it perpendicular to the line, thereby creating an extra arm.” I waited for someone in the group to notice the new sum. 

It didn’t take long for a fifth grader to notice that all of the sixes add up to 30 points. “Turning the Double on its side, created a fifth number to add. Since all of the numbers were the same, you can’t help but have a multiple of five! It is literally five of the same number.” 

I tried the word problem on my daughter Scarlet who had a brilliant reason for using the Double instead of the 2-6. In addition to the points, you would cause your opponent to have to take from the Boneyard, because chances are they won’t have a six. Limiting their options was very strategic thinking. I shared this strategy with my 4th graders who already knew the game well.

Next, it was 2nd grade’s turn. These kiddos had just learned how to play the game for the first time the day before. I used the word problem to reteach some of the ideas. More than focusing on problem-solving, I walked my second graders through the mechanics of writing a word problem. We discussed the details of Dominoes that I included in my little story. “Why did I mention multiples of five?” I prompted. “The goal is to earn points.” 

I had toyed around with the idea of only having words. When I originally crafted the word problem, I didn’t have the Dominoes laid out on a table. I tried to provide just the right amount of text for students to be able to visualize all of the details necessary for solving the problem in their heads. At the last minute I decided to include a photo with the problem. This was only the third day I was teaching these students! Watch out, though. Word problems, here we come! 

Pride flooded my person when fourth grade arrived in my room and crushed this problem within seconds. I’d taught all but two of these students how to play Dominoes last year. When I saw how quickly they solved the puzzle, I wished I’d hidden the photo. 

I pointed out the verbiage at the end of the word problem. “Why is it okay that I didn’t say what numbers were on the Double in the word problem?” I asked them. I had left out this vital information on purpose, and I wanted to see if they could find the puzzle within the puzzle. I did this kind of trick with them all last year. They understood that it had to be two sixes because the word problem stated that “You have two bones that you can play.” If the double were any number other than six, you couldn’t play it.

Here’s a question I failed to float: “Is it possible that the player has more than two Bones?” And, this is where a photo is limiting. Because you can see only two Bones on the table, it is difficult to imagine there being more than two. But, yes, the parameters of the problem leave that detail open. You have two that are “able to play,” but you may have more. I’ll have to work that riddle into a future problem!

My last group of the day was third grade. Here, I used the word problem differently. After exploring the numbers and solving the puzzle, plus revisiting how to play the game, I drew their attention to the structure of the word problem. It was a story, providing characters (you and a friend), a setting (a game of Dominoes), and a conflict. “This word problem has a plot,” I pointed out. (Plot is the language arts concept that third graders are learning right now.) 

The problem of which Bone to play is the climax of our story. The resolution is a mystery. You could use either Bone. Which one is better? What is the third, less obvious option? How will the story end? 

And, this is the end of my blog about this amazing word problem. But, is it? Through the process of fleshing out the many lessons that coated these Bones, I have come up with some additional puzzles. Here is a taste: “What is the highest score that can be collected in one play of Dominoes? What would the Bones look like at the ends of each line of play?” I think I’ll provide manipulatives; Bones; for pupils to push around when solving this. Good luck!

Parameters Are Classy

I could get all educational-philosophical here, but really, I just want to share an awesome lesson. You know I would love nothing more than to explore the paradox of limitations providing freedom. And, I’ll definitely be looking up the etymology of parameter, but first…

Friday, September 15, 2023, was the last day of an incredible week of transition. Due to health complications, my good friend Julia Dweck is not going to be teaching the gifted students of Willow Lane this fall. (Please consider donating to her Go Fund Me.) I will be filling in for her.

That means someone has to fill in for me. The Polite Pirates (my 3rd graders) are lucky to have Julia Lutz at the helm! She began transitioning into captain of my class on Tuesday, following Monday night’s school board approval. 

While it may have felt like a roller coaster ride of a week, it definitely wasn’t one of those vintage, wooden, chiropractor-necessitating coasters that loosen your molars. I recently visited Hershey Park with my family. My daughter Scarlet and I went on every single roller coaster. Her favorite was the Jolly Rancher Remix. I think she liked the dance music and lights. I enjoyed Farenheit. It was fast, loopy, and thrilling. It also looks cool from the ground. 

Handing my class over to Ms. Lutz was like watching a Hershey Park attendant safety-check my daughter’s harness and start a ride that we knew would deliver amazing thrills through scaring the wits out of us! It was clear at the onset that Ms. Lutz has better classroom management than I ever did. The Polite Pirates didn’t just obey and listen. They modeled the essence of respect when Ms. Lutz spoke to them. The cart on the track of this winding, hilly year was obviously a safe place, even if it was going to climb a very high hill and plummet toward earth at an incredible velocity. 

And now for the lesson. Friday afternoon Ms. Lutz, myself, and Cassie Doemling (East Penn HS field student, basketball player, and Polite Pirate; Cassie was a student of mine a few years ago;) brought the Polite Pirates on a treasure hunt. 

When I explained to the 3rd graders that, “We are going to be hunting in a place that is dangerous for humans, so we have to send in robots,” eyes understandably widened. Ms. Lutz opened the Spheros case, and everyone “Oooohed” and “Aaaaawed” at the lights. I swear a couple of Spheros shook with excitement, as well! 

We had torn five large, different color rectangles of poster paper off of rollers in the hall earlier in the day. While Ms. Lutz demonstrated how to program a Sphero to a circle of students sitting on the carpet, I drew giant Xs on the other papers. One student from each of 5 groups would get their iPad and download the EduSphero App. Then go to Ms. Doemling to retrieve a robot. The groups of students were coached on how to work as teams. Then they were off!

The first hunt was pretty easy. Students had to get their robot from the center of a circle to a giant X painted on the opposite side of the paper. The Sphero had to simply touch the X. It did not have to be in the middle. It was basically a straight line. 

As it turns out, the introductory coding you get when you open a new program, the very first time does exactly this. It sends the robot on a straight line away from you, and brings it back to its starting point. The Polite Pirates had to adjust the duration and direction. I told them to make the speed 30. 

Once a team was successful in reaching the X that marks the spot of treasure, I introduced an obstacle. Cassie and I had made a bunch of piraty problems prior to the lesson. We had a different one for each team; There was a great white shark, a storm cloud, a mean-looking jellyfish, and a threatening pirate. Now, the obstacle was placed in the middle of the poster paper island, and here are the parameters:

  • The Sphero must get from its starting circle to the X without leaving the paper. 
  • It cannot touch the problem.

They were simple. They were measures of success. More than limitations, the parameters were goals. “Can we do it while meeting these demands?”

As teams began to experience successes, Ms. Lutz stopped everyone to both congratulate their progress, but also share some important news: “What good is a treasure that you can’t spend? You need to get your Sphero back to the circle. The starting point is your way off the island.” Now, students had to figure out a round-trip route. 

Because this was now Ms. Lutz’s “show,” I left Room 207 before the teams had completely finished their hunts. It felt like exiting an awesome roller coaster ride. I knew I could get back in line and go again, but was happy for the people who would experience it next. What a fun experience! 

Persephone Play

When you mention Greek Mythology in a 3rd grade classroom, students get all excited. They have heard some of the famous names, like Zeus and Poseidon. They might be familiar with Mount Olympus and the idea of characters (gods) having powers or being responsible for natural phenomenon. Very few have ever heard any of the specific stories.

I recently shared a play with the Polite Pirates (my students) that I’d written a few years ago. Originally, I wrote it to be performed during a winter holidays celebration. It is the story of Persephone being kidnapped by Hades, causing her mother Demeter (goddess of the harvest) to get so depressed that she allowed the whole Earth to wither and die (Winter).

After reading it through once, students switch parts. It is okay for a girl to play Hades, the richest of the gods (he is governor of all the Earth’s minerals… gems) and a boy to read Demeter (goddess of the harvest), etc.

Before creating teams of four to read the play, I explained a little about Greek Drama. Rather than have a narrator, there is a “Chorus” that sings the narration. As you can well imagine, this was a silly experience. We read the entire play through once as a class. I had to count to 3 each time the Chorus was “singing” so that we were somewhat together.

One other thing that I incorporated into this drama that was very different was having two groups reading/performing at the same time. This is called dual dialogue. It can be difficult to pull off, but the text lends to rich teaching opportunities. Why would Hades and Zeus be talking at the same time as Persephone and Demeter? Where might they stand, if this was being performed on a stage?

I had to point out the comedy of some of the dialogue and stage directions. Even though you read the text within parenthesis to yourself, and not out loud, it is important to actually read it and imagine what is happening in order to get the point of the story. And then, I made the chorus use hyperbole in its declarations, along with some fourth wall breaking when Hades interacts with it. With these explanations, a little coaching and modeling, we had a lot of fun reading this play. I welcome you to use it (Google Doc of play) in your classroom. It’s a great end of the year activity.

The subject of being kidnapped and taken to the underworld, albeit very dark is made light with loads of comedic relief. Also, I incorporate a game of Monopoly, so that 9 year olds have more to connect with.

Cast of Characters:

CHORUS – the voices that narrate the play 

PERSEPHONE – Goddess of Spring, daughter of Demeter

DEMETER – Goddess of the Harvest, sister of Zeus & Hades

HADES – Ruler of the Underworld, brother of Zeus & Demeter

ZEUS – Leader of the Greek gods & ruler of Mount Olympus (also, Demeter and Hades’s brother)

CHORUS: (As if making an important declaration; introducing a dignitary) Who is more powerful than death? He comes to take us all. NO THING can escape him.

HADES: (Pretending to be humble) Well, you know… I am pretty powerful…

CHORUS: There isn’t a living thing that can withstand your power, oh mighty Hades!

HADES: (seems a little uncomfortable) Yeah, well, that is actually part of the problem.

CHORUS: Hades, ruler of the Underworld, keeper of secrets, all powerful bringer of…

HADES: (cutting CHORUS off, mid praise) Yes, yes, yes… that is all great, and everything, but keeping secrets is not all it’s cracked up to be. 

ZEUS: Are you complaining, brother, Hades? I thought you liked being all-powerful ruler of the Underworld.

HADES: Oh, hi Zeus. It’s not that I am complaining or anything. I’m just a little lonely down there, all by myself… me and my secrets… You know.

CHORUS: Hades, lonely, desperate, seeker of companion…

HADES: (interrupting what seems to be an increasingly negative appraisal of himself) No, no, no… It’s not like that. I’m not desperate or anything… 

ZEUS: (in a soothing voice) Do you need a friend, brother? I’ve been noticing you leave your Underworld unattended to visit Mount Olympus more often recently.

HADES: (kicks the ground sheepishly) I just see Demeter and her daughter having such a nice time together. All I ever hear are tree roots growing. The only beings I can talk with are the worms of the ground.

ZEUS: You signed up for that job. You wanted to be (exaggerate importance) “All Powerful”. I let you rule down there, even though I didn’t think it was a good idea. 

HADES: I know, I know. Okay, you’re going to make me say it: I wish I had a friend.

CHORUS: (jeering tone) Hades, wants a friend! Hades wants a friend! Hades wants a…

PERSEPHONE: (to Persephone) Did you hear that?

DEMETER: No, what?

PERSEPHONE: It was probably just the wind.

CHORUS: (very quietly, as if from far away) Hades, wants a friend! Hades wants a friend! Hades wants a…

(Here, two separate speaking parts happen at the same time. Take turns speaking, but make it obvious who you are talking to.)

HADES: Oh brother… 
ZEUS: Do you need a shoulder to cry on?
HADES: No, I need someone to share secrets with. They are no good all bottled up inside!
ZEUS: Are you asking me to send someone down to the Underworld to keep you company?
HADES: That’d be nice.
ZEUS: Who do you have in mind?		PERSEPHONE: There it is again.
DEMETER: I didn’t hear anything.
PERSEPHONE: I think I want to go check it out, mother.
DEMETER: I don’t know, Persephone. I have quite a bit of harvesting left to do here. I will be sad without you.
PERSEPHONE: I won’t be long. I just feel like someone is in need.
DEMETER: Don’t be gone long.

PERSEPHONE: (not seeing Hades who is walking away, backwards) Hello? Anybody there? …Boy it’s dark down here…

(Hades moves away from Persephone as she moves closer to him, until she bumps into him.)

HADES: Oh, hi there.

PERSEPHONE: Were you the one calling on the wind for a friend?

HADES: No, that was the Greek Chorus. They narrate Greek plays.

PERSEPHONE: So, you weren’t the one in need of a friend?

HADES: Well… (a little embarrassed) I’m not going to turn you away.

PERSEPHONE: What’s your name?

HADES: Oh, excuse me, where are my manners? My name is Hades.

PERSEPHONE: Aren’t you the ruler of the Underworld?
HADES: (a little shy) That isssss  technical my title…
PERSEPHONE: I bet you get lonely down here.
HADES: You could say that.
PERSEPHONE: Do you play board games?HADES: I’m bored all of the time!
PERSEPHONE: No, board games, like chess, checkers, Monopoly….
HADES: (excited) Let’s play Monopoly!
PERSEPHONE: That sounds fun. I’ll be the top hat. 
HADES: That’s classy…		DEMETER: (looking for her daughter) Persephone? Where are you?Where did you go?
Zeus, where is my daughter? 
ZEUS: What’s wrong, Demeter?
DEMETER: I’m looking for Persephone, and can’t find her.
ZEUS: (thinking to himself) Hmmm, I wonder if Hades brought Persephones to the Underworld to keep himself company.
DEMETER: The Underworld! WHAT?!
ZEUS: (sheepish) Well… Hades was feeling lonely.
DEMETER: (to everyone/threateningly) I am not going to let anything grow again, until Persephone returns to me.
ZEUS: (soothingly) I’ll talk to Hades.

CHORUS: And, Demeter, true to her word, neglected all plants and animals while she searched for her daughter; Field and forest dried up.

ZEUS: (observantly) This is not good.

CHORUS: Demeter looked everywhere for an entrance to the Underworld, by which she might fetch her daughter. 

ZEUS: (speaking to Hades) Um, Hades… excuse me.

HADES: (speaking to Persephone) That’s your third roll, and no doubles. 

PERSEPHONE: Ah, man! Now, I have to pay the $50 to get out of jail.

I’m hungry.

HADES: (speaking to Persephone) I’ll go get you something to eat. 

ZEUS: (speaking to Hades) Hades, we have a problem.

HADES: (notices Zeus) Oh, hi Zeus! Persephone and I are enjoying a game of Monopoly. Do you want to join us?

ZEUS: I’d love to, but I can’t. Wait, how long have you been playing this?

HADES: Oh, I don’t know. Maybe three months or so. 

ZEUS: That’s a long game! No, I can’t join you; Demeter is so upset at Persephone’s disappearance that she has refused to allow the earth to rain or grow or live this whole time.

HADES: That doesn’t sound good. I thought the Underworld was getting more action than usual. 

ZEUS: I’m sorry, but Persephone needs to go back to her mom.

CHORUS: Hades agrees to send Persephone back to her mom, but first gives her 3 pomegranate seeds.

PERSEPHONE: Thanks for the nachos, Hades. They were a little crunchy, but yummy. 

CHORUS: The pomegranate seeds caused Persephone to remember her Monopoly game with Hades.

HADES: Come play Monopoly with me again, Persephone.

CHORUS: Demeter was overjoyed when she saw Persephone… So happy, in fact, that not only did all of the plants grow back, but they grew beautiful flowers.

DEMETER: I am so happy to see you!

CHORUS: Now, every year, Persephone visits Hade in the Underworld during the winter months. Her absence causes Demeter to get depressed…

DEMETER: I get so depressed.

ZEUS: This causes everything to die. 

PERSEPHONE: The world goes cold.

HADES: We play Monopoly for three months every year.

DEMETER: When my daughter returns to me it is like she springs out of the earth.

CHORUS: This is how the ancient Greeks explained the seasons.

May the 4th be with You: Symmetrical Starships

Today was May 4th… No, it was May THE Fourth! As in, “May the fourth be with you…” This meant the Polite Pirates (my students) simply had to do some Starwars-themed activities.

In preparation for a fun puzzle project, I taught the Polite Pirates about symmetry. I told them that they would be drawing spaceships. They were very excited.

“There is a reason the wings of an airplane are symmetrical,” I began. “Have you ever seen this trick?” I asked my class, taking a piece of paper and placing it just below my mouth. 

As I blew hard right over the top of the paper, the entire paper flew up and fluttered under my breath. “Oooohs” hummed across the room. 

I drew a picture of the paper on the board and explained, “When air travels quickly across the top of the paper, you create a vacuum (Physics Force, 2023). The fast moving air pulls the air that is resting in front of the paper up to join it. With no air in front of the paper, it gets sucked up into that empty space. 

Without any good pics of my teaching from earlier, I reintroduced the lesson right before dismissal to snap this photo of amazement.

“Your household vacuum is a machine that creates a vacuum in order to suck up dirt and dust,” I tell my students. “A motor spins a fan that pushes air out of the machine. When the machine is empty of air, that is when it is truly a vacuum.” Mouths make Os of understanding. 

I drew a crude picture of an airplane wing. “When air flows under the wing, it is going straight. That part is flat.” I draw arrows of air moving straight. “The front of the wing curves up and back. Air has to bend and is angled up when it travels over the wing. This causes the air that is resting above the wing to travel up also, creating a vacuum, or low pressure. As the air goes up, the wing goes up (Shaw, 2021).”

I picked the piece of paper back up, and once again demonstrated air pressure pulling the paper up. Of course, they all wanted to give this a try! After a minute or two of varying successes, I drew an entire airplane on the board.

This Polite Pirate planned out his space craft on paper before arranging polygons on paper.

“If one wing were smaller than the other, the plane would raise unevenly,” I explained. “The aircraft would start spinning. It is important for the wings to be symmetrical, so that the airplane remains balanced.” 

[All of this explaining took longer than I had planned, but it was worth it. The students were really into the science of “lift,” and it lended extra importance to the idea of symmetry.]

After attracting the Polite Pirates attention once again, I explained, “You are going to engineer your own starship space cruiser,” I whispered in a serious, hushed voice. “The main quality that your creation must have is symmetry. Whatever you design on one side must exist on the opposite side of your ship.”

Tracing the shapes with pencil proved tricky.

Each student received one large piece of paper. Students could work in pairs if they liked. Bowls full of plastic polygons were placed in the middle of groups of desks. The Polite Pirates took several polygons each and began assembling space ships. 

I had told them and wrote on the board; At least 8 polygons per ship, and at least 3 different shapes must be used. 

Students were to hold down the plastic shapes with one hand, and carefully trace an outline of the perimeter with pencil. Then they removed all of the polygons and went over the pencil with a marker. 

“You will trade your picture with a partner and try to recreate each others’ space ships, arranging the colorful plastic polygons on the papers,” I explained. 

Students took photos of their creations, so that they had answers to their puzzles.

Creativity swept the classroom! Colorful space cruisers covered desks and flowed across the floor. 

This Polite “Padawan” Pirate even drew an insert to show the movement of her spaceship.

A pair of students asked me if their shape was symmetrical when they had to add a blue triangle to a row of parallelograms in order to make a long thin trapezoid. I told them to ignore the color. “Can you cut it in half and fold the one side on top of the other hiding it completely?” When they saw that they could, they realized the symmetry of the shape. 

The one thing that I’d do differently is limit the number of shapes. While my students had a blast using tons of polygons to make gigantic space ships, the answers to puzzles were too open-ended. A student could use a hundred combinations of shapes to fill a large empty space. The better puzzles were the ones that had a set answer.

It would have been better for space ships to have only a few right answers. Then the refilling of the perimeter with colorful polygons would require more concrete problem-solving.

All in all, this ended up being a memorable, fun learning experience. The Force was very strong with all of the Polite Pirates today.

Sources:

Physics Force. University of Minnesota . (2023). Retrieved May 4, 2023, from https://physicsforce.umn.edu/content/paper-lift-0

Shaw, R. J. (Ed.). (2021). Dynamics of Flight: Kids Page. NASA. Retrieved May 4, 2023, from https://www.grc.nasa.gov/www/k-12/UEET/StudentSite/dynamicsofflight.html#:~:text=Airplane%20wings%20are%20shaped%20to,wing%20up%20into%20the%20air.