Tag: STEAM

How Much STEAM Do Your Lessons Contain?

How do you challenge yourself as a teacher? I’ve been working on making my pedagogy more powerful by pushing lessons forward with STEAM. Originally known as STEM (Science, Technology, Engineering, and Math), STEAM introduces the Artistic element to the closely related fields. When you are teaching a STEM subject, it is common to integrate more than one letter of the acronym (Hertz, 2016), but one of my modus operandi is to try to incorporate as many of the letters as possible into any given lesson. Powering my teaching with as much STEAM as possible is an art form to me.   

I sometimes use art as a reward for completing work. “Once you finish solving the math, you may draw the aliens you encounter on your adventure!” I told enrichment students at the beginning of this math lesson.

Some lessons are more successful at incorporating all five letters of STEAM than others. A recent math lesson got my creative juices flowing, and turned into a beast of learning for my 4th grade gifted students. It all began with an enrichment lesson from Ready Math. 

4th grade gifted students use art to get even more out of STEM.

Fourth graders had been reviewing place value as well as adding and subtracting large numbers. This is the perfect example of a math concept becoming boring for advanced students, those who have shown mastery of the subject matter. Once these kids conquer the use of algorithms, plugging in numbers to get sums and differences becomes mindless. Adding and subtracting is like riding a bike. Why make them pedal a stationary one when we could take it on a trip, instead? This is where I come in. 

My first stop on developing math enrichment lessons is to check out the iReady Teacher Toolbox for ready-made resources that I may build upon. Curriculum Associates, the makers of Ready Math, has developed an enrichment assignment accompanying nearly every lesson. These are worksheets that can be printed for students to work on independently. You can push the assignment out digitally via Google classroom, too. The Ready Math team has provided a “Teacher Version” that contains answers; Even potential answers to open-ended questions, so that teachers know what to expect!

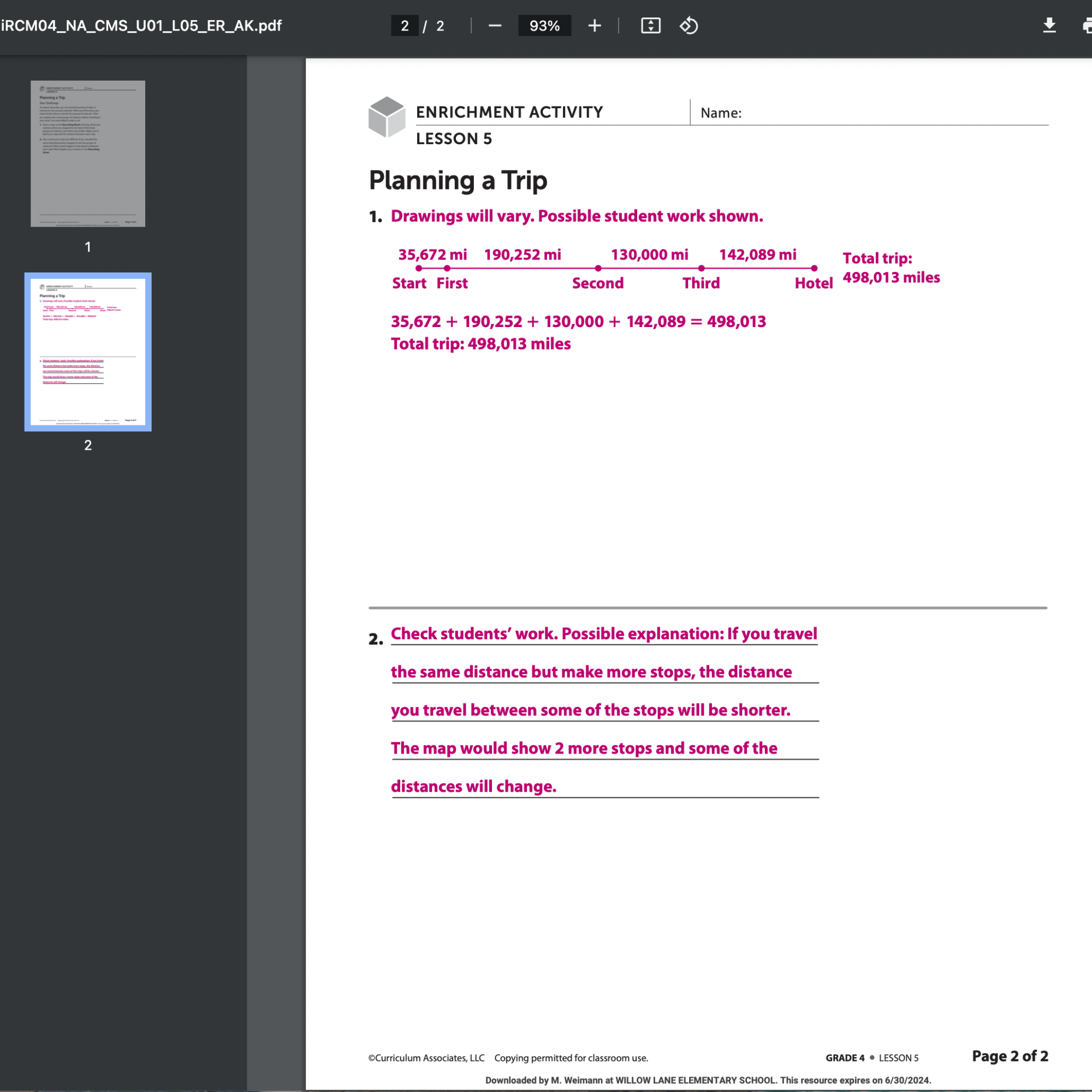
For this lesson, I took a screenshot of an iReady enrichment assignment, and used it as the background of a Google Jamboard. I like Jamboards because my students can draw and write on their iPads. They can create new blank slides, as well as duplicate the one with the instructions on it. It is easy for me to make a template, and then create a copy for each student through Google classroom.   

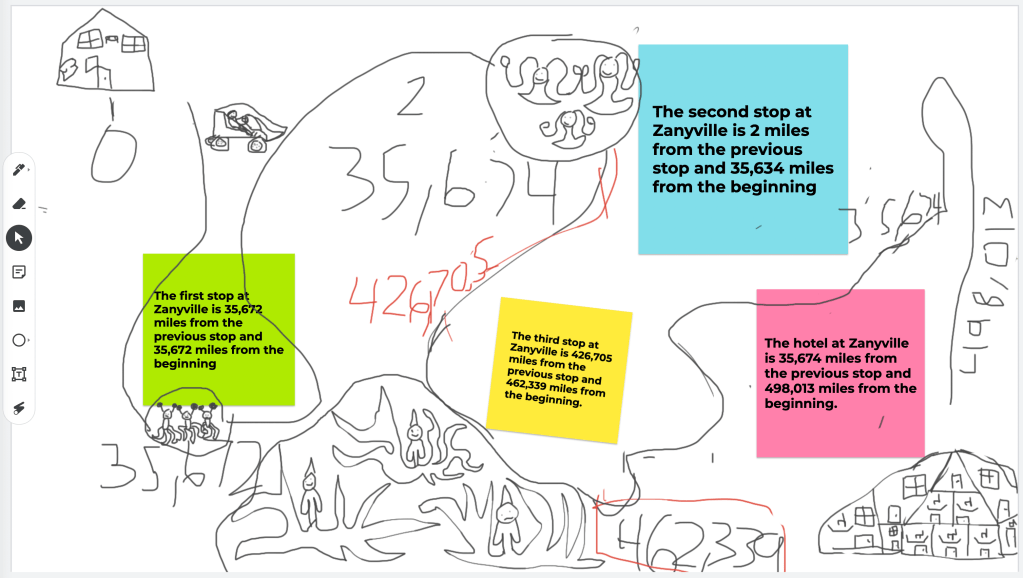
This zany lesson, “Planning a Trip,” had students pretend to explore an imaginary planet, Zanyville. It introduced gigantic numbers and was very open-ended. I included some more instructions that I shared orally, when I initially rolled out the project. “You must tell me the number of miles from the beginning of the trip where each of the stops happen. Also, you have to provide the distance between the stops.” Students were instructed to use “sticky notes” in Jamboard to share this information. They showed their work on other slides.

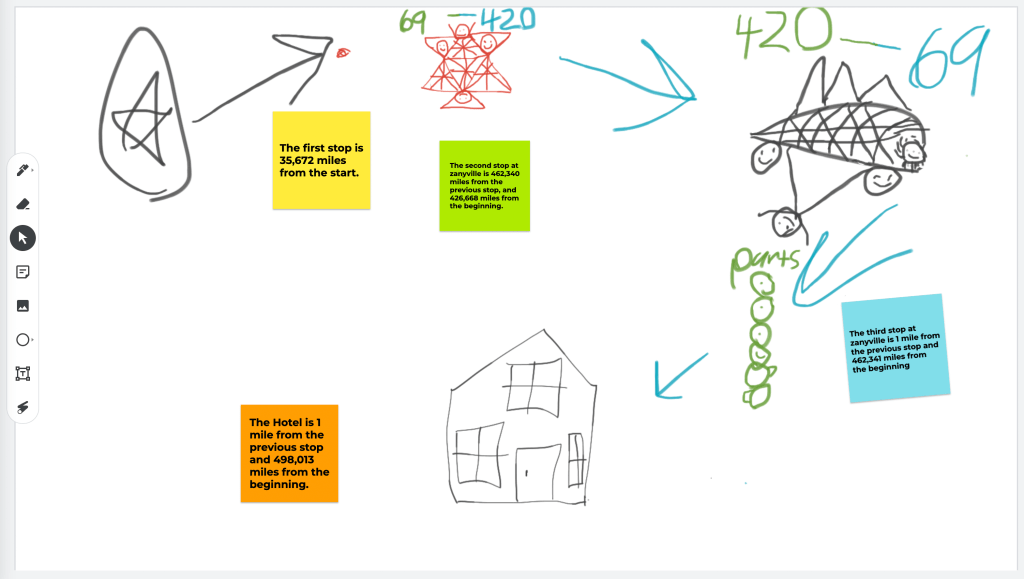
The 4th graders worked hard and were engaged in making their maps. Only, the maps were grossly disproportionate. Some students made the third stop only “one mile” from the end of the trail, but placed it a fifth of the distance from it along the route they drew in their Jamboard. In actuality that distance would represent tens of thousands of miles! It is true that I did not instruct students to partition their maps with accuracy, but when I witnessed the misuse of proportion, I saw a fertile opportunity for learning. Enter, STEAM!

My vision for math enrichment is to dig into each concept, finding riches that deepen the understanding of my students.

The next time that I met with the 4th grade math enrichment students, I taught them proportionality. There weren’t any Ready Math lessons on this, but it fulfilled my mission for the enrichment group perfectly! My vision for enrichment is to deepen students’ understanding on math concepts. We do not rush ahead or necessarily “do more” math. I try to present novel ways of using the concepts that students are learning in the classroom. Sometimes, lessons include real-world problems, using the math that they are learning to perform a task they will most likely encounter some day. Other times, we may play a game that requires students to view the numbers in a unique way. In this instance, I wanted my enrichment students to learn about the relationship (ratio) between numbers.

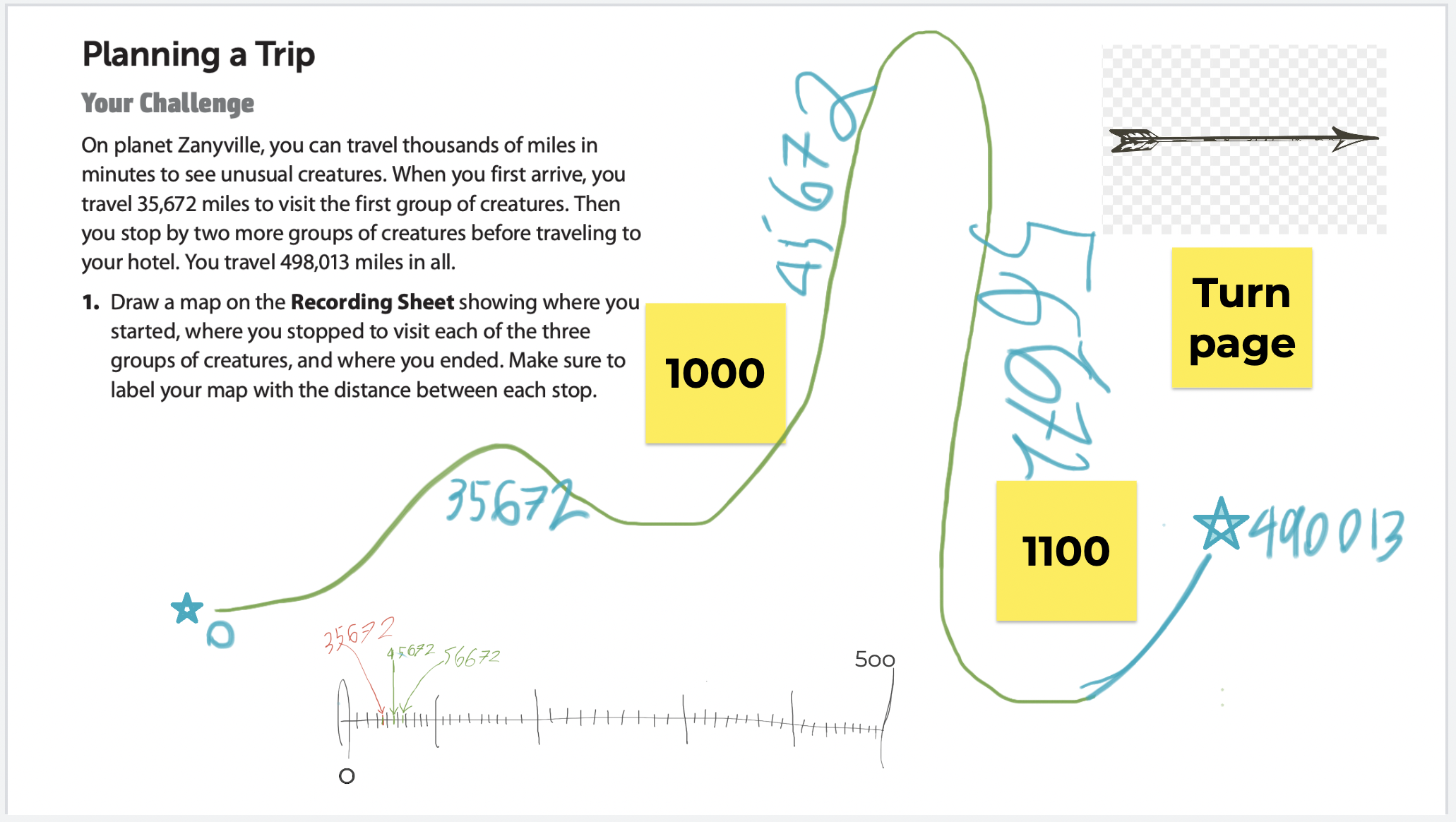
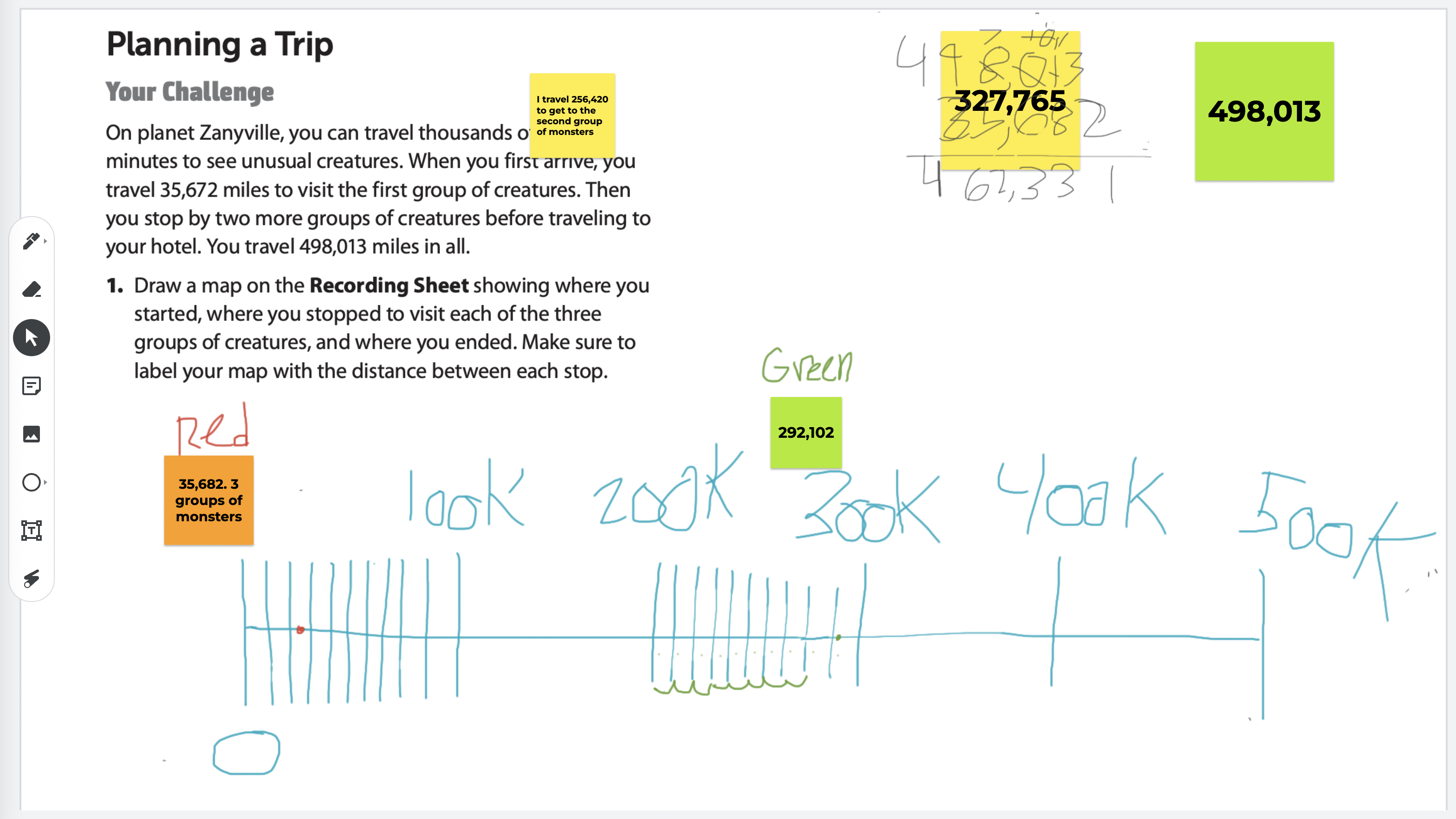
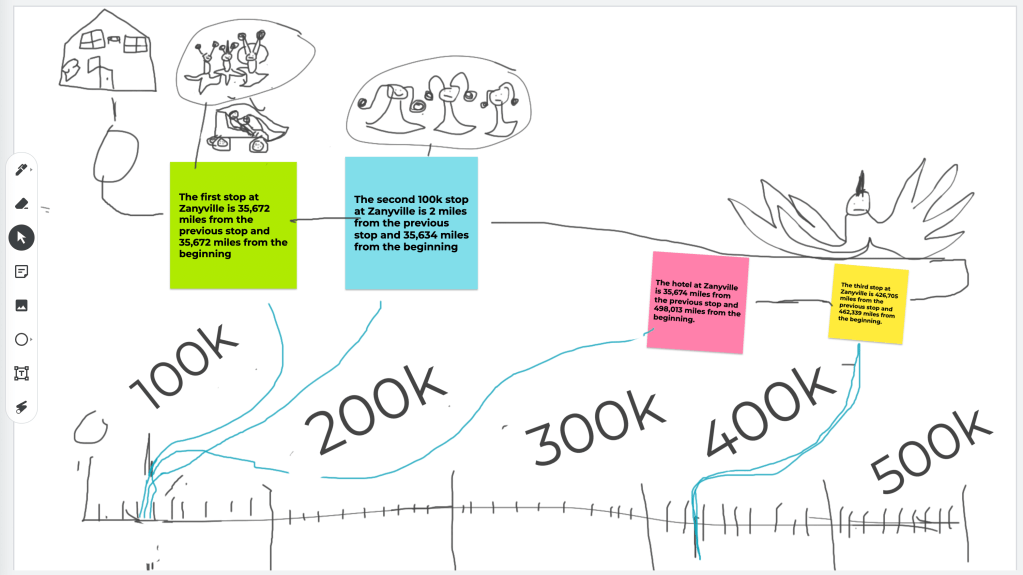
I modeled partitioning a space on the whiteboard. With students’ input, I placed numbers in appropriate places on the makeshift number line. After a short lesson on this, I had students revisit their “Planning a Trip” lesson from the previous week. They were to make a number line and show where each stop would happen. Their Google Jamboards showed excellent progress in understanding this concept.

From Enrichment to Gifted Instruction

This is where the lesson took a turn from enriching math understanding to present problem-solving and higher-order thinking through gifted instruction. In order to illustrate the disproportionality of the original maps, I’d have the gifted 4th graders use one of their own to display an accurate account of the journey.

How would we do this? I would lift the trail from the map. The trail would become a rope that could rise up off of the map. This would allow my gifted students to account for extra mileage and figure out how someone may have covered the distance of tens of thousands of miles, but look, from only glancing at a two dimensional map, as though they had only hiked a handful of miles. My plan was for the fourth graders to learn about topography.

I gave my students a rope that was about 50 feet long. Their initial task was to tie pieces of yarn onto the rope symbolizing stops on the trip. They used what they had learned from the previous math enrichment lesson to do this.

“If the entire trail was 498,013 miles (this was on the planet Zanyville, remember), and the first stop was only 35K miles from the start, you couldn’t mark it halfway along the journey!” I reminded them. 

We brought the rope into the hallway, so that we would have plenty of room to #STEAM. The first thing my students did was section the rope into five equal parts. It being a 50 foot rope, each of the five sections was ten feet. As it turns out, the tiles in the hall were one foot wide, so each one symbolized ten thousand miles, nicely. Once we had some reference points, we figured out where each stop would be and tied a piece of yarn to represent the place. 

I then took one of the disproportionate maps that one of the gifted students had drawn, and I enlarged it onto poster paper that covered a large portion of the classroom floor. Next, we placed the rope showing our well-proportioned stops onto the map. We taped the pieces of yarn to the stops drawn on the map. There were huge portions of extra rope between some of the stops, and it was too short in other places. 

I asked my students to “Imagine that this rope isn’t a rope, but a journey. Someone actually did travel these miles, and they traveled along the route that is represented on this map,” I told them. “How could this be?” Their first idea was that the “journey” coiled around and around; As in, the traveler had actually walked in circles. “There is a loop drawn on the map,” I pointed out. “You should assume that the line drawn on the map is the exact path the person traveled.” I wanted them to discover the concept of elevation on their own. 

“The journey (they were very keen on calling the rope ‘journey’ and yelled at me when I mistook it for ‘rope’;) goes up!” several students shouted in unison. Feigning surprise, I encouraged my students to show it. I told them to make it happen. “Elevate the rope to show traveling up off of the paper.”

Watch the time-lapse of my 4th grade gifted students creating a model of their journey.

The students started grabbing everything within reach to raise their “journey” off of the paper. I gave them a few parameters: They could use anything in the room, other than my personal things. It had to follow the line of the map. The journey has to stand independently. “It can’t need you to hold it.” I heard the students mentioning how much fun this was several times, as they stacked Rubik’s cubes, built structures out of KEVA planks, and draped rope Journey over the 4’ high faux pilings I’d made for another project.

After finishing, I asked “How could we show these mountains on a two-dimensional map?” This is where topography enters the scene. Before exploring the topic, I had the gifted students brainstorm ways to display three dimensions on a flat piece of paper. They came up with drawing small images, like triangles symbolizing mountains. Information in a key was paramount. I showed them some maps that had varying colors used to illustrate elevation. They liked that idea. Finally, I introduced contour lines. These are drawn around the mountains, and show the incline of the slopes.

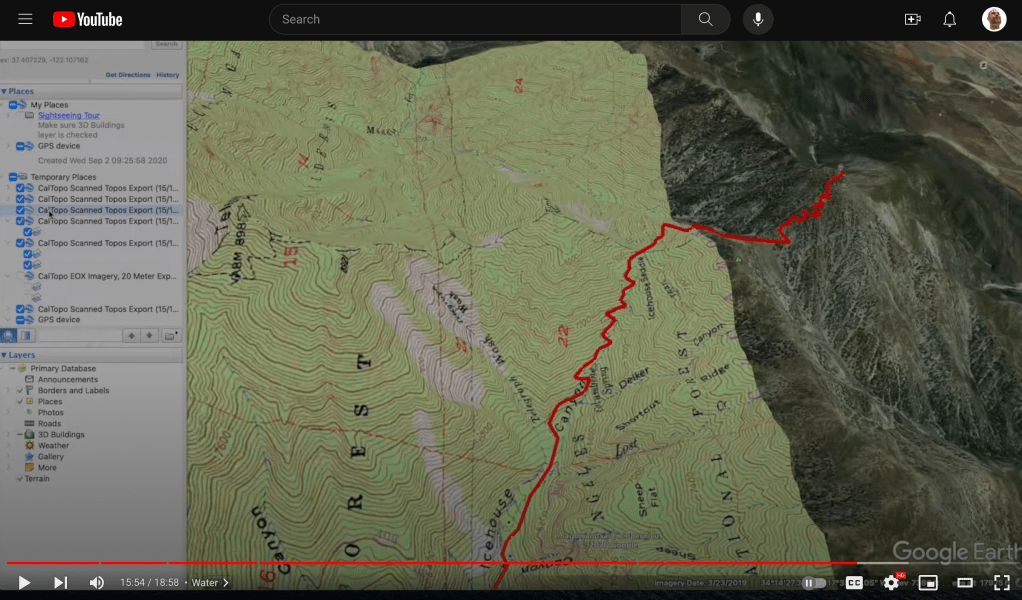
Once I did my best to explain how contour lines worked, I showed my students a video (above) made by HikingGuy.com. In the film, “Hiking Guy” takes a two-dimensional, topographical map and imports it into Google Earth Pro. He overlays the topographical map onto the exact geographical area that it represents. With Google Earth in 3D mode, the Hiking Guy swivels the view, so that you can see the depth of the mountains and valleys. We were in awe of the effects. I could have told my students that a contour interval is the amount of elevation between two contour lines on a given map, but seeing it displayed via three-dimensional modeling drove the concept home.

Next, it was time to collect some data to use in our map-making. We used yardsticks to measure how tall our mountains were. (I would have used centimeters as the measuring increment, in order to keep with everything scientific using the metric system, but since the Ready Math assignment had started the project off with “miles” on Zanyville, we kept to the standard system.) Before clearing away all of the materials elevating our journey, we marked the beginnings and ends of each mountain along the route on our map. In this way we would know the edges of the bottoms of our mountains for drawing contour lines.

Prior to drawing our contour lines, we needed to figure out what our contour interval would be. The first thing we did was figure out the height of each mountain, according to tens of thousands of miles. If a mountain is only nine inches high, as was Mount Rubik’s (we named all of our mountains), and a foot (12 inches) represents ten thousand miles, what is the elevation of the summit? We figured out that nine inches is 3/4 of a foot, so we concluded that our nine inch mountain was 3/4 of ten thousand; or 7.5 thousand miles high. The taller mountains required us figure out how many feet fit within the total number of inches. Some rounding was used, and we came up with some valuable summit information that was transferred to the paper map.

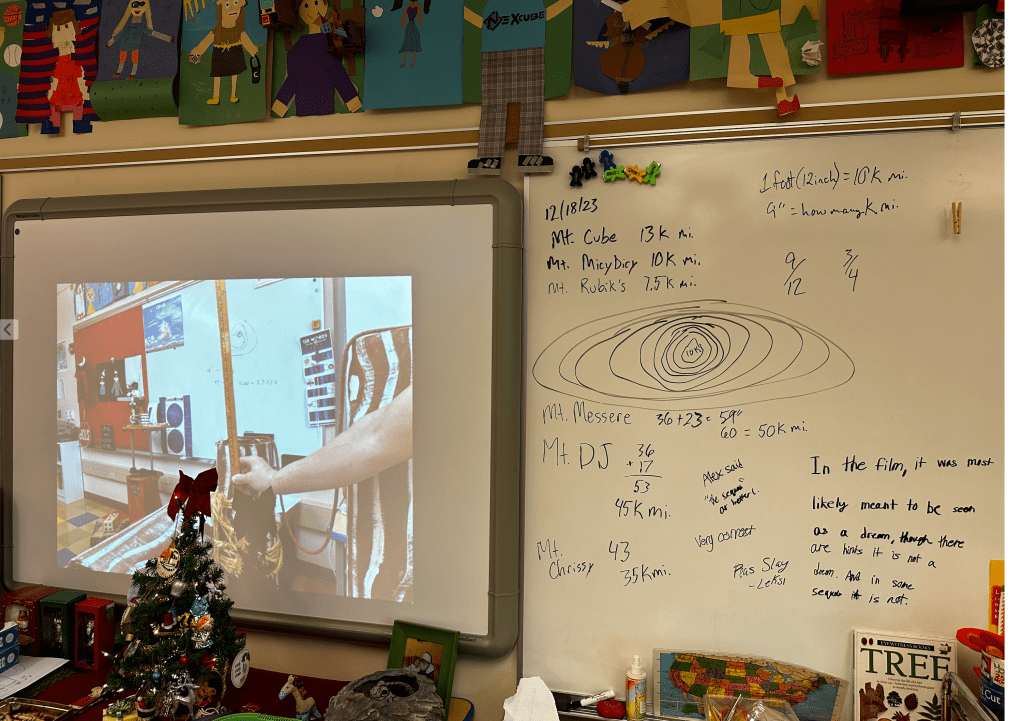
Now for our contour interval. How much elevation should each space between contour lines represent? We want the lines to be meaningful, but too many would make the map cumbersome to produce as well as read. We took each of our summits and found a number that was doable.

STEAMing Up Your STEM

Believe it or not, including art with the traditionally scientific fields of STEM has been mildly controversial. “The focus of STEM is developing rigorous math and science skills through engineering. How can you focus on other subjects (such as art) without losing the mission of STEM or watering down its primary purpose?” (Jolly, 2014). People who think this way are trying to isolate the left side of the brain (Pietrangelo, 2022). They imagine that opening STEM up to the arts would allow right-side brain activity to infiltrate and weaken STEM, but Jolly (2014) points out that this is viewing it all backwards. Art is already used in engineering, product design, creative math, and out of the box science. Strengthening our artistic use of STEM will make all four subjects so much more powerful.

Slow cookers like crock pots use lower heats to cook food over longer periods of time, deepening flavors and breaking down meat muscles, so that food becomes soft and tender (2022). A pressure cooker, on the other hand, cooks meals much faster. This mechanism has a seal that helps maintain the pressure within it. Steam builds up and pushes into the meats and other ingredients, breaking down the foods to make them tender, as well as infusing the flavors. You may not have tons of time to teach a STEM lesson. Use art to make the learning more memorable.

Saunas are small rooms that are heated up to 160 Fahrenheit. The health benefits of sitting in one of these hot beds for a short amount of time include clearing the pores of your skin, relaxing muscles, and burning calories, as well as increasing blood circulation (Hussain & Cohen, 2018). Add some water to the hot rocks in these wood-paneled spaces, and you have yourself a steam room. A steam room can help clear ones sinuses, loosen joints, and repair broken skin tissue (Johnson, 2023). [One thing to watch out for in a steam room is dehydration. It may seem ironic to dehydrate when surrounded by so much water, but the heat will cause moisture to leave ones body. Make sure to drink plenty of water and keep your time limited.] Using art in your lessons can add health benefits to your teaching. Students who favor their creative right side brain work might remember the lesson more. The artistic element could clean out misconceptions for visually-oriented students.

The difference between STEM and STEAM is as subtle as sauna vs steam room and slow cooker vs pressure cooker. I’d say that teachers are most likely using some art in their STEM lessons… I can also imagine a STEM teacher feeling pressure to utilize art which could lessen the lesson. Does titling teaching “STEAM” allow for art, promote its use, elevate art to STEM prominence, or simply point out the fact that it was there all along?

I like to think of art as the glue that holds the Science, Technology, Engineering, and Math together. I’m surprised we could see out the windows; There was so much STEAM happening in our classroom!

Enriching the Enrichment

A lesson that I began in the middle of this long mapping of a “Journey” project involved slope measurement. I thought that figuring out the value of the angles of the mountains would be useful. As it wasn’t helpful in completing the drawing of our map, I dropped it after spending only a little time on it. The information was very interesting, however, and I can foresee using it in on a slightly different angle of the lesson; Switchbacks.

Our Journey would not have gone straight up the sides of the mountains. A switchback is when a trail travels at an incline, but also more parallel than perpendicular to the mountain’s rise. After a short distance, the trail will “switch” directions and zig zag up the side of the incline. This means that the hiker will walk a much longer distance in order to get to the top of the incline, but it is an easier hike. What does this mean for our Zanyville trek? The journey, being its given length, will not go up as high; This will lower the peak or summit of each mountain. But, by how much?

Students can explore steilhangs, learning more about earth’s geography. Furthermore, they could research the differences between Earth and other planet’s geographies. 

I had students conduct a scientific examination through dropping small plastic cubes on top of one another to form a miniature naturally formed mountain. They were not allowed to touch the mountain with their hands. What was the angle of elevation? We placed a ruler parallel to the side of the slope and used a protractor to measure the angle of elevation. It was about 15 degrees. 

It will require some advanced geometry to recalculate the distance from the base of the mountain to the summit, given new measurements of switch back angles and lengths between directional changes. I might incorporate these elements to the lesson when I do it next year. It’s time to wrap this up.

Finally, I would like to see my students graph the elevation of the trip. Between zero miles and 498,013 miles, where did the trail rise and fall, and how much? 

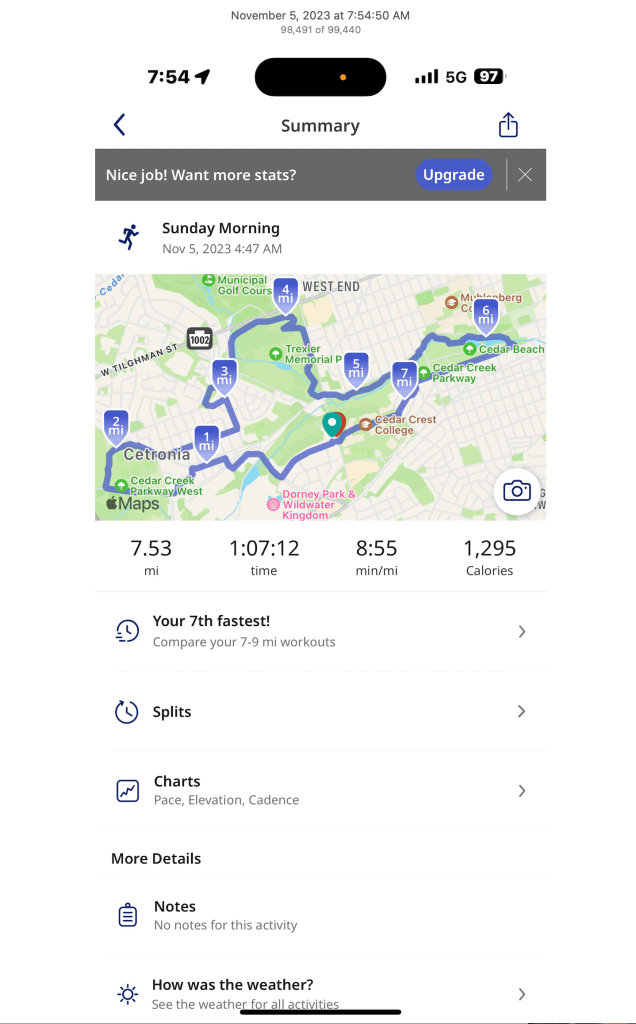
I use a running app that uses GPS to track my progress. It calls out my splits at five minute intervals. It also provides charts showing variations in my speed, cadence, and elevation. I want my students to create an elevation chart similar to the one from my running app. It ought to display where the traveler would begin and end hiking up/down mountains, as well as how high the peeks were.

Here’s a spectacular video displaying a taste of the elevation I experience on my runs in the Lehigh Valley, PA.

Sources:

Hertz, M. (2016, February 1). Full STEAM Ahead: Why Arts Are Essential in a STEM Education. edutopia . https://www.edutopia.org/blog/arts-are-essential-in-stem-mary-beth-hertz#:~:text=In%202006%2C%20Georgette%20Yakman%2C%20a,the%20traditional%20STEM%20curricular%20areas.  

Hussain, J., & Cohen, M. (2018, April 24). Clinical Effects of Regular Dry Sauna Bathing: A Systematic Review. National Library of Medicine. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5941775/#:~:text=Facilities%20offering%20sauna%20bathing%20often,%2C%20stress%20management%2C%20and%20relaxation.

Johnson, J. (2023, December 7). What are the benefits of a steam room?. Medical News Today. https://www.medicalnewstoday.com/articles/320314

Jolly, A. (2014, November 18). STEM vs. STEAM: Do the Arts Belong?. Education Week. https://www.edweek.org/teaching-learning/opinion-stem-vs-steam-do-the-arts-belong/2014/11

Pietrangelo, A. (2022, May 9). Left Brain vs. Right Brain: What Does This Mean for Me?. healthline. https://www.healthline.com/health/left-brain-vs-right-brain

slow cooker vs pressure cooker: what are the pros and cons. Farmison & Co. (2022, November 11). https://www.farmison.com/community/blog/pressure-cooker-vs-slow-cooker

Building Bridges: A Hands-On Math Lesson

This blog serves two purposes: First, I just shared a lesson with the Polite Pirates (my class) that went so well that I want to share it with everyone. And, second, due to its complexity, several students need additional clarification. I am hoping that by writing this down, I can make clear how the business of bridge-building works.

Yesterday morning I dug out the colorful, connectable, plastic blocks I’d stored away in a bin under the counter. I told my students that they would be building bridges. Cheers rang out. They were to work as a team to construct a way for a car to travel from one pile of dictionaries to another. The Polite Pirates cheered with joy.

“There’s a catch, however. You have to buy the blocks!” I exclaimed. The class groaned. “Each one costs ¼ of a dollar. (I’ve been teaching fractions and mixed numbers.)”

“How much is that?!” a few students grumbled.

“You know how much a quarter of a dollar is,” I accused. 

“Twenty-five cents?” a student clarified.

“Yes. You will work as a team of engineers. Use your Spiral Notebooks to keep track of the number of blocks. You’ll need to figure out the total cost of your bridge.

“Oh, one more thing: Your bridge is going to make you money. That’s right! Sure, it will cost you to build it, but once it is done, you can charge a toll for cars to use it. For every foot of bridge you are allowed to charge one dollar. 

Making money got their attention;)

This is the slightly confusing part (one of them, anyway): If about twenty vehicles travel across your bridge per hour, how long will it take to make (dramatic pause) one thousand dollars? 

Before setting them loose, I showed them that this problem was doable. (The looks on their faces were incredulous.) “Let’s say you build a 10 foot bridge. How much money can you charge to cross it?”

“Ten dollars.”

“Right, but that is $10 per car. If twenty cars travel across your bridge in one hour, how much money do you earn?”

Thinking… “Two hundred dollars,” a student offers. 

“Good; You are correct. Where did that number come from?” I prompt. I want the class to know how to do these calculations.

“I multiplied ten by twenty.”

“Right. If your bridge makes $200 every hour, how long will it take to get to a thousand dollars?” Their minds were working, now! 

“Five!” several students shouted in unison. 

“Don’t forget that you need to use some of that money to pay for the building blocks that you used to construct the bridge,” I remind them. And, they’re off! 

The Polite Pirates had a blast working together. I was impressed that they almost instantly formed the idea of making supports to hold up longer sections of bridge. In this way they could earn more toll money. Of course, they had to count the blocks that they used to hold up their bridge when tallying up the cost of building materials. I didn’t let them use anything other than the building blocks for construction. 

Once the bridges got to be several feet long, every single student on the team was needed to hold the bridge in place as more supports and lengths were added. I overheard one third grader explaining to his partners that even though it would cost more to use extra blocks, they would make more money from tolls, because they could make their bridge longer. I reinforced this idea by sharing, “Sometimes you have to spend money to make money, folks!”

After a timer I had set went off, I had everyone stop building and count up the number of blocks that they had used. One team split up the task by divvying up the sections to be counted. They then added all the numbers together. Next, it was time to calculate the cost of all of those blocks. One team had used 355 blocks! How could they figure out 25￠ per block? 

I reminded them that they already knew what a quarter of 100 was. “Separate the 300 from the 55,” I told them. “Each 100 would be how much?”

“Twenty-five dollars,” someone answered. 

“That’s right. Now, how many twenty-fives do you have? We’re talking about 300 blocks.” I wrote 100÷4=25 on the board. When someone suggested that they needed 3 twenty-fives, I put X3 under the 25. “These might seem like really big numbers, but you already know what ‘three-quarters of a dollar is,” I prompt.

“Seventy-five cents!” a few blurt out. 

“Not cents, though…” I can see the gears turning behind my students’ eyes. It feels like I can hear the steam coming from their ears. They even gasp with understanding. 

“Seventy-five dollars.”

“Now, for the 55 other blocks. Is there a number close to 55 that is divisible by four,” sounded like Greek to them. I reworded my question in a more leading way. “Can 48 be evenly divided by 4?” This connected with their math facts. A student raised his hand.

After deciding that 48 blocks would cost $12, we tackled the leftovers. “What’s left?” I asked the Polite Pirates who were sitting so patiently on the carpet in the front of my classroom. Counting up from 48 to 55, we discovered there were seven blocks left. “How can we figure out the cost of these?”  

When this question was met with blank stares, I quickly drew seven (very ugly) squares on the dry erase board. I drew a hasty circle around the first four. “Each of these cost 25￠. How much money is four quarters?” Lights blinked on in every students’ eyes. 

“One dollar…!”

 “And…” I prompted for the cost of the remaining three unaccounted for blocks. 

“A dollar and 75￠,” a student finished the thought.  

“So, these seven cost $1.75, the 48 blocks cost $12, and the 300 blocks cost $25 X 3,” I summed up our calculations thus far. “What will this team need to do next? Tell the person next to you.” Then I sent everyone back to their seats to work out the costs of their bridges. I told them to figure out the prices independently. Then compare your work with your teammates. In this way you can double-check your math accuracy. 

I walked around the room, helping students with their division facts. There was a wonderful hum of productive struggle. Some individuals figured out that they would have to add more than one additional hour on to their original answer in order to account for the cost of the bridge. Most found that only one hour would do the trick. 

Now that all of the math was done, it was time to write about it. I had posted a question in the Polite Pirates’ Google classroom: “How long will it take for your engineering firm to make one thousand dollars?”

They could work with partners and discuss their writing with their team, but each student was responsible for producing their own explanation of what they did. I left the math that I’d shown them on the board, so they could copy it into their notes, or just write about what we figured out together. 

One of the things I like most about using Google classroom on iPads is how easy it is to use the “Speak to Text” feature. It’s true, you have to teach and practice rereading and editing your text, in order for students to use this effectively, but it speeds up typing entire paragraphs. It also helps facilitate a more “Discourse” -style text. When my students purely type, they are less likely to include opening statements, and they will leave out key details. Through the process of “Telling” their iPads what they did, you get a more structured description. And, because it is easy and fast to do, students don’t have a problem including more details. 

Here are just a few samples of the amazing answers that the Polite Pirates typed into their Google classroom assignment.

I hope you enjoyed hearing/reading about this lesson that my students experienced this week. If you have ideas on ways to improve or modify it, let me know in the comments. Thanks, and take care.

Mission Impossible: The Engineering Process with SpheroEDU

IMG_8638
Is your “mission” to get kids excited about learning, or is it testing?

“I have a math test to give you, but I thought we could program some Spheros instead,” I said Friday morning to applause from the Polite Pirates of Room 207. Students’ cheers gave way to music… Mission Impossible Theme Music! 

“Your mission, should you choose to accept it… And, you’re going to want to accept it… is to rescue people from certain peril,” I proposed. With everyone on the carpet, I explained that before a rescue, engineers would set up models that they could use to plan out their efforts to minimize loss of equipment and life. Their mission was to program Spheros to make it through a model of obstacles, getting to someone or group of people who needed help. The Sphero couldn’t stray from the path or touch the walls because it would be damaged and not be able to complete its mission. 

Screen Shot 2019-11-09 at 7.19.04 AM
I walked them through what they would experience.

The students were riveted to my instruction as I taught the “Engineering Process” that they would need to use while figuring out the most effective code for completing their rescue. This was the real reason for the lesson, but simultaneously they would get so much more out of learning/practicing coding, problem-solving, and working together in a team. 

I went over each scenario, pointing out the “criteria” and the “constraints”, two vocabulary words from the “Engineering Process” model from Foss Science. Students whispered with neighbors about which they were more interested in trying. I told them that if they mastered one, they may move onto another “Mission”. 

Students then returned to their seats to get out their math spiral notebooks for taking notes about how they used the “Engineering Process” while solving their missions. They opened the Google slideshow that had all of the missions, as well as an image with the Engineering Process in it. I had “made a copy for each student” through Google classroom. 

I pulled popsicle sticks with student numbers on them to pair kids. As numbers were drawn, pairs came to the carpet to redeem their Sphero robot. Then they chose whatever mission fancied them most. With two pairs per mission, the class was a buzz of engineering within moments.

IMG_8633
“The Medic was difficult, but a lot of fun,” one student told me as I circulated the room.

 No one got to complete more than one mission, and most did not completely finish every parameter I had set for them, but every single student was 100% engaged in a learning activity full of purpose. 

IMG_8622
The problem-Solving was explosive!

I want to back up to the beginning of the day, before I tell you how this memorable lesson came to a close. Students entered my room to find me painting posters. They asked what I was doing. Because I didn’t know exactly what to call it, I didn’t give them a straight answer. That drove them crazy. They asked to help. “Sure,” I answered, getting out more paint brushes, cups and paints. All I had to do was outline things, and kids would fill in. When I told them that the white was snow or that the red was fire, it fueled their curiosity all the more! Dave Burgess calls this “Preheating the Grill” (Teach Like a Pirate, 2012). My students were so hooked on this upcoming lesson, they hardly wanted to go to gym! Have you ever heard of such a thing? 

While students were at their special, I made some finishing touches and turned a fan on to help the paint dry quickly. Then I came up with names, stories, and varying parameters for each mission. I took pictures of the maps, typed up the scenarios, and threw together a slideshow to share with the class.  

Back to the lesson. Throughout the “Engineering Process”, while students were working on coding Spheros, I stopped everyone a couple of times to instruct them to take screenshots of their code. That way they could have snapshots of different levels of success. It would help them describe their problem-solving, later. Finally, I put together a Flipgrid for students to make selfie-videos describing how they used the “Engineering Process” to solve (or come close to solving) their mission. If they finished, they could watch their peers’ videos and comment. 

IMG_4422
I didn’t even realize that this was National STEM day! (November 8th, 2019)

We DID take the math test, but in the afternoon. They did fine. I’m sure they will remember that forever;)