Tag: math

Pedagogical Aikido

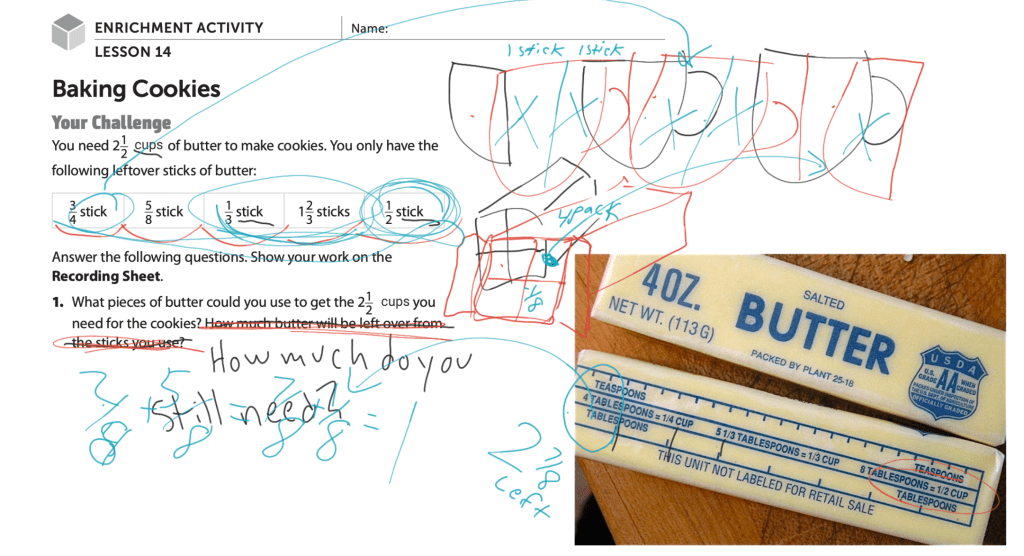
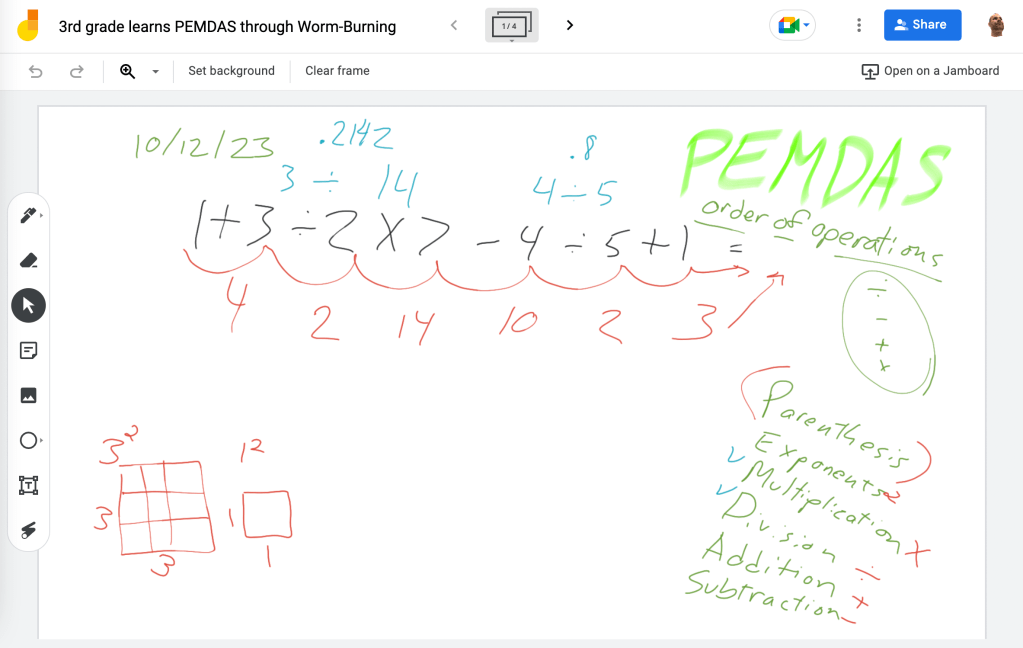
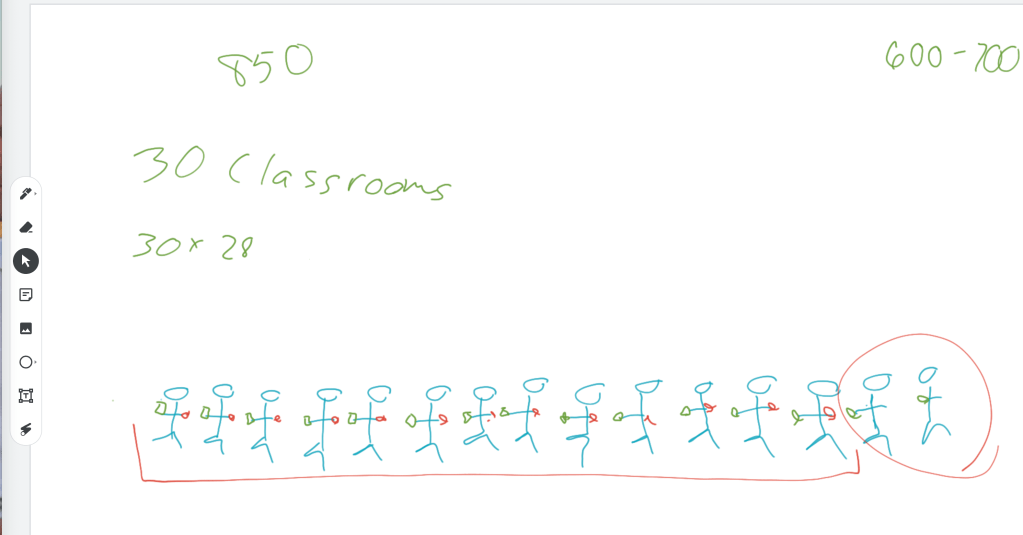
“Where did the 850 cans come from?” I was in the middle of sharing the iReady enrichment lesson (14) with my fourth graders when one of them asked me this question.

Have you ever had a student ask a question in order to postpone learning? If you’re a teacher, then that’s a silly question. Of course! 

This is one of the few things that I remember from my elementary and middle school days. It was a thrilling challenge to try to come up with just the right topic or question that could throw the teacher off track. 

We would hope and pray for a story. Then, we would artfully flatter and ask questions that would lead our pedagogue down the rabbit hole of memories, further and further… away from the lesson at hand. 

Fast forward forty years. Today’s students still play the same tricks on their teachers! This past week I was engaging some fourth graders in math enrichment, when one of them tried steering me off task. Little did they know, that I practice Pedagogical Aikido. 

Redirecting Energy

Aikido is a form of martial arts that is known for using an opponent’s energy (ki) against them. Masters of this study practice redirection. 

Although I have not formally studied Aikido, I love its principles and attempt to use the philosophy of redirecting thought and energy within the walls of my classroom as much as possible. 

For example, the other day when my student asked about the origin of the 850 cans in our math problem, I allowed the student to think that he had derailed the lesson. I told him that this was an excellent question. “850 cans is a lot of cans. Where would a school get that many cans for a fundraiser?”

The martial art Aikido uses a triangle to teach the redirection of energy. There are three components that work together to use an opponent’s attack against them, saving your energy and neutralizing the situation. It all starts with Balance, known as tachi waza (Aloia, 2020).

“How many students does our school have?” I asked the class. 

I could have squashed the student’s inquiry, telling him something like, “I don’t know where the number of cans came from. It’s hypothetical. Let’s just move on!” Or, “It came from Curriculum Associates, the authors of our math program. Don’t ask silly questions.”

If I had done that, I would have disrespected the student. A dismissive teacher or one who blocks the question head on is too hard, too strong; the lesson too one-sided. By allowing for the question in the first place, and then entertaining it, I had my center of gravity low to the ground. My metaphorical feet were spread wide apart and knees bent. The question didn’t topple my lesson. I was balanced.

In answering my question, the students were surprisingly accurate. Our school has around 700 students. “How many cans would we have if each student brought in one can?” I prompted. That was easy. “But, not every student will bring in a can… And, some will bring in more than one.” The easy back and forth of these simple concepts established a flexible, down to earth ease of thinking. It also revealed the problem. We don’t know where the 850 cans came from.

Next, it was time to Break Balance. This is the second part of the redirecting-energy triangle. “The opposite of balance is imbalance, or kuzushi. To break an opponent’s balance, one must first redirect their energy to one’s own advantage” (Aloia, 2020)

I shouldn’t be surprised, but I was very impressed, nonetheless, at how quickly my students figured out how many classrooms our school had. It was the advanced fourth grade math students receiving enrichment, after all!

I had begun the imbalance kuzushi by getting the class to come up with the total number of classes in the building. After figuring out that our school has five classrooms per grade and our school teaches six grades, if you include kindergarten, we discovered that there are 30 classes represented.

“Let’s say that our school collected 850 cans. How many cans would each class bring in?” The students had no clue where to start.

Antonio Aloia (2020) explains that kuzushi has two arms. The physical off-balancing of an attacker, parrying the opponent’s strike and redirecting the momentum of the assault, coupled with a strike of their own is what one normally thinks of when imagining Aikido. Um, of course there isn’t any literal physical contact with students, let alone “attacks,” but presenting this new problem of dividing up the number of cans by the number of classrooms was a cogitational assault of sorts.

The other arm of kuzushi is a psychological off-balancing. This is where a martial artist would “Distract a would-be opponent by bringing their attention to something else, be it an object on a building or something farther away and behind the opponent” (Aloia, 2020). Pedagogically, this happened when I changed the student’s original question from “where” to “how”: “Where did the cans come from?” turned into “How could a school come up with so many cans?”

While the martial art of Judo involves throws, Aikido keeps your opponent tight and controlled. Perhaps counter-intuitively, it is concerned with the well-being of the attacker. So, rather than toss my students aside to flounder with the problem of dividing 850 by 30 on their own, I guided them through the process of figuring out the answer.

I asked them how many cans there would be if every class brought in 10 each; 300. “Okay, maybe that was the first week of the fundraiser. If each class brought in another ten cans during the second week, how many cans would the school have collected?” We were up to 600 cans. They were starting to catch on. 

One of the students used Google to divide 850 by 30. Rather than scold him, I asked him if it were possible for any of the classrooms to bring in .333333 of cans. This was a silly question. “What happens with the remainder from the division answer?” I asked. They didn’t know. “For our purposes, we will assume that the students from every classroom brought in 28 cans. The teachers brought in the rest.” My students were okay with this explanation. 

The third side of Aikido’s redirecting energy triangle permeates everything. It is ki or energy. Don’t think of it as power or force, though. Ki is more like momentum.

“How big are our classrooms? How many students are there in a classroom?” I got several answers on this. We decided to use the number 20. “Let’s say that a quarter of the students don’t bring in any cans. If the rest are responsible for bringing in 28 cans, how many brought in two and how many brought in one?” My students just looked at me. I told them to try and figure it out on their own, and then I’d show them. 

One student crushed it, and I had her show the class what she did. Then I modeled drawing a picture to solve the problem. 

After all of this, I told my students, “Now that we have collected all of these cans, we need to put them in something to bring them to the food pantry that we are donating them to.”

“If Dylan went out and bought a bunch of boxes… Thank you Dylan! (Dylan is all smiles at this point; He may or may not have been the person to ask the question that started all of this;) And, if Dylan’s boxes are all the same size, holding six cans each, how many boxes would Dylan have to get?” I let them wrestle with that a little while. 

When I was prepared to let them demonstrate their math on the board, I turned to the slide that had the original question on it. They reread the word problem as I decided on who would come forward to share their work first. A few students groaned and some others called out. “That’s the problem we just did!” 

“Yeah?” I feigned ignorance. 

I used someone else’s name when I told the story about getting bigger boxes; Ones that held 8, instead of 6 cans. “How many of those boxes were purchased?” 

As it turns out, we never got to fully explore the last question, but a couple of students tried solving it in their heads. I had completely Aikido-ed them! Lol.

Redirecting energy can be an even more effective motivator than a cool lesson. Take their energy, spin it around, and use it against them. Students will feel like they’re in charge of their own learning, and in a way, they are!

Source

Aloia, A. (2020, June 19). Reflecting on Jujitsu Pioneer George Kirby’s Advanced Techniques for Redirecting an Opponent’s Energy. Martial Arts of Yesterday, Today and Tomorrow. https://maytt.home.blog/2020/06/19/reflection-on-jujitsu-pioneer-george-kirbys-advanced-techniques-for-redirecting-an-opponents-energy/comment-page-1/?unapproved=2695&moderation-hash=f6966939a4ca212a2123a94cabda8d13#respond

Buttery Batch of Math Cookies

This is the introduction that I used on my fifth graders.

In preparation for teaching a math enrichment lesson to my fifth graders, I looked at the iReady “Extension” activities in the Ready Math “Teacher Toolbox,” and I found a problem that I liked a lot. (iReady and Ready Math are products of Curriculum Associates. My district has been using it for several years, and I like it a lot.) This lesson (14) is all about using fractions to solve word problems.

Here’s an image of the worksheet that a teacher could photocopy or share via Google classroom. Because I have the luxury of actually teaching enrichment lessons, I decided to do some explaining before handing over the problem. Also, I opted to make a few tweaks, too. In my experience recipes usually call for specific measurements of butter, not a number of “sticks.” Therefore, I covered up the word sticks in the problem and wrote in “cups.”

This changed the outcome of the answer quite a lot. Now, students would not have enough butter to complete the recipe. They could access new sticks of butter, but if they did that, then solving the problem wouldn’t require wrestling with all of the fractions presented in the partial sticks. That’s when I imagined the real-life experience of baking cookies after having worked all day at making a big meal, like Thanksgiving.

Needing soft butter for recipes is a real thing. Also, who doesn’t love consolidating? We can clean up all of those partial sticks of butter and make cookies at the same time!

I shared what a typical day of cooking in preparation for a large Thanksgiving meal looks like at my home with my fifth grade students, setting the stage for having several fractions of sticks hanging around. With the instruction to use up the warm butter first, and then dip into the cold butter from the new package, I set my students loose to calculate how much butter would be left.

Many students jumped on adding up all of the fractions. They began figuring out compatible denominators, so that they could combine every partial stick and find out what they had in all. “But, do you have to do that?” I asked them. No one wanted to venture a guess.

“What are you asked to find?” I pressed.

“Two and half cups of butter,” someone accurately answered. Without saying anything, I drew two of the worst cups ever drawn on an interactive board, followed by half of a third. I made fun of my drawings, which everyone helped with, pitching in their own digs. Once that settled down, I pointed out the lines I’d drawn through the middle of each measuring cup.

“Why’d I do that?” Earlier, we had discussed that fact that one entire stick of butter was the equivalent of half a cup. The students understood better than they could put it into words, so I articulated the concept for them, “Each half of a cup was one stick of butter.”

Then, we looked back at the fractions. It was easy to see that 1 2/3 + 1/3 would be able to fill one whole measuring cup. That leaves us with three fractions with differing denominators. “Before working out a common denominator to add up all three, think about what you are trying to do,” I instructed. “What is your aim?”

I showed the students that 1/2 a stick of butter + two of the 3/4 would equal one whole. “That would take care of half of a measuring cup,” I told them. Also, I should mention that I crossed out halves of measuring cups, as we discovered combinations of partial sticks of butter that would fill them.

“If we used up two of the quarters to combine with the 1/2 a stick and create a whole stick, how many quarters are left?” One quarter. “And then, we have 5/8 of different stick left.”

They instantly got it. We were 1/8 short of a whole stick of butter. In the end we needed one whole cold stick of butter, plus 1/8 of an additional stick to add to all of our warm butter fragmented sticks to fill our two and a half measuring cups.

The Ready Math extension lesson (14) has a second question that I left as is. The catch is that my students used our additional left over cold butter (2 7/8 sticks) from my adapted first problem to solve it. I let them struggle with this one for a few minutes before I showed them the short cut of drawing pictures.

“You might think it childish to draw pictures,” I began. Fifth grade is the oldest grade in my school, so these were the seniors of the place. “…But, I find it easier to manage some problems when I sketch what is happening.” I had been watching them crunching numbers, making common denominators again, and subtracting fractions. Now, within a handful of seconds, I showed them how many quarters could be made from two sticks of butter! I pointed out the idea of labeling the quarters in order to keep track of my thinking. I wrote a B above each “batch” of cookies. Sure, I could just count the quarters, but when it came to the last stick, it will be important to identify what portions of butter will complete a batch.

As I divided the last rectangle into eighths, I asked, “What am I doing to this last stick of butter?”

Rather than answering my question, they were chomping at the bit to be the first to spew the solution to the problem. “Eleven and 1/8!” more than one fifth grader shouted at the same time.

“No, that’s incorrect,” I casually, but cautiously counseled. Rewording what they had yelled in order to make plain the problem with their answer, I said, “You cannot make 11 AND 1/8 batches.” The emphasis on the word “and” did the trick.

“You can make eleven batches, and you’ll have 1/8 of a stick left over,” a student corrected.

“Perfect,” I affirmed. “Drawing pictures might seem silly, but look at how simple it is to see the answer. We didn’t do any denominator work past doubling up the number of sections in the last stick. I hardly did any math, beyond simply counting!

“When you are taking standardized tests, you get scrap paper. Use it. Draw pictures. Illustrate word problems. Take the time to label parts of your illustrations. Make sure that you understand what you are being asked. What is your goal? What are you supposed to find? It’s not just a number. It is the solution to a problem. In real life, it is a key that will unlock a problem. Be a problem-solver; Not a human-calculator,” I told them.

Photo by Elliot Fais on Pexels.com

In conclusion, my aim is to turn these advanced math performers into problem-solvers. With this goal in mind, I try to make lessons that force students to use what they have learned in their regular math class in a way that is not only compatible with what they would find in the “real world,” but forces them to understand how to use the skills. I often allow my students to use calculators because the problems I prepare for them require more knowing what to do with the numbers than practicing running through algorithms. AI can learn how to crunch numbers, but will it be able to successfully manage a kitchen full of amateur chefs laughing, telling stories, and making meaningful memories, all the while measuring butter for cookies after already cooking and eating a Thanksgiving dinner?

To combat the threat of AI, don’t try to make humans better than machines. That just makes them more like machines. I say, grow the human-ness of students. This is getting pretty deep, so I’m going to go eat a buttery cookie while I chew on these ideas for a future blog;)

Wallpaper Based Learning: Math Enrichment

Who wants to see a picture of Mr. Weimann with hair?

EVERYONE, apparently. I used this hook to get students to pay attention to my pitch of wallpaper hanging. They hung on my every word. 

This was a math enrichment lesson, in which I presented a real world problem that my fourth grade advanced math students would struggle through, using many math concepts that they already know. Knowing what to do with the numbers is sometimes more than half of the problem.

When I was in college (the first time;), I began painting to pay my way. Back then, it was just the outside of homes (exterior painting). Upon graduating, I conducted an informal internship with a wallpaper hanger. He taught me all about interior painting; which is VERY different from slapping paint on siding; and he trained me to hang wallpaper. 

This pic is from 20 years ago.

I was 22 years old, had long, curly, brown hair, and according to my students who did end up earning the privilege of viewing my old photos, quite tan (nearly all of them commented on this fact;). I worked with the professional wallpaper hanger for a little less than a year, hanging all kinds of paper in all kinds of homes. 

About half of his work came from a restoration company that did insurance projects. These homes had suffered water, smoke, or fire damage.

Unlike a company that specializes in a niche of upper-middle class single family repaints, this work brought us into a wide range of residences. I worked in downtown Philadelphia and on the Main Line, a very wealthy area–This place has both Ferrari and Lamborghini dealerships, among others!

This was one of the stranger bathrooms I papered. I had to paper inside that skylight.

We rehung thick, tough paper on basement ceilings; and metallic, mirror-backed papers in tiny bathrooms. It wasn’t unheard of for me to have to remove several layers of paper in older homes, in order to get to a clean plaster surface. 

It was fun to see so many different types of homes, meet a variety of peoples, and travel all over the area. I learned a lot about problem-solving because every job was completely different, and you didn’t get paid until it was done, and done well. 

Eventually, I struck out on my own. I got married in 2000, and my wife Sonia and I started our own painting company called “Excellent Painting.”

We used feathers to produce the veins on this marbleized pillar.

We ordered lawn signs and door hangers, spread the word, and pioneered a full-service painting/wallpaper business that did it all! We even dabbled in faux finishes, popular at the time. Faux finish is when you use tricks and artistic techniques to make pillars and walls look like marble, stone, or wood.

Because we were the only company that could do all three, we got a lot of business, especially in the new developments that were popping up in suburban areas near where we lived. The market was ripe, and we were busy. 

This is a photo of one of our neighborhoods. We would literally move our equipment from one house to the next, working our way around the loop. Having the interior of your home decorated by Matt and Sonia Weimann was a must.

There are many components to running a successful business. You have to market the company, spreading the word, so that people know to call you. Then you need to return phone calls and perform estimates. Those estimates need to be cheap enough that people will hire you, but expensive enough to cover the costs of supplies and provide a livable income.

Eventually, you have to deliver on your promises. You have to be able to successfully perform the work that you estimated. Be prepared to follow up on complaints, questions, and problems. If you don’t, an infection of bad publicity will spread around the neighborhood, and you can write that group of homes off! Do things well, and reap the rewards of moving from house to house, cutting down on marketing costs and time. 

This is an advertisement from a small local paper that was mailed to many homes in our area. It was an awesome investment!

Many of the skills and lessons that I learned through entrepreneurship are tapped in my teaching. Some days the professional world mixes with pedagogical practice more than others. My favorite place to bring my background to life is in math lessons. 

The other day, I treated my fourth grade math enrichment class to a treat of problem-solving that had them working hard, thinking hard, and learning hard. The challenge was to help me come up with a price for wallpapering a couple of bathrooms.

I shared a photo of a bathroom that I papered several years ago. Many opinions about the bathroom were unsolicitedly shared by my students. In order to get them motivated, I asked, “Who wants to see a picture of Mr. Weimann (that’s me;) with hair?”

Instant quiet. Hands involuntarily went to mouths to clamp lips shut.

“Listen up.” I proceeded to explain that you don’t just glue wallpaper to walls. You have to perform all kinds of preparatory work. 

There’s taking down old paper, because many times the rooms that you are going to hang wallpaper in were rooms that were already wallpapered. This is a lot of work. You may not know this, but wallpaper is two layers. There is the thin vinyl layer that sometimes peels off in large flexible sheets, but other times has to be slowly, painstakingly, curse-your-existence-ly chiseled off of the walls in tiny, bitesize pieces; As, you can probably tell, I have had too many experiences like this! Then there is the backing, which more closely resembles actual paper. This, you wet and scrape off rather nicely. There are all kinds of tricks to removing wallpaper more efficiently, but suffice to say, you better estimate plenty of time for this part of your project!

Sometimes I used a steamer. Other times you can just spray warm ammonia water on the wallpaper.
More often than not, you just chisel away at the top layer.

You aren’t done preparing the walls for wallpaper when all of the old paper is removed, however. Before you move on, you have to clean off all of the old glue! If you don’t, your new paper may not adhere properly. You do not want your new wallpaper to fall off the walls or bubble up. This process is not only messy. It can be deceiving. The glue is transparent, so that it does not discolor the wallpaper. Cleaning it off of the walls requires diligent and frequent assessments. Run your fingers over a cleaned wall. If you feel anything slippery or slimy, it is probably glue that still needs to be scrubbed off.

People don’t hang wallpaper the way they used to. My students will probably never practice this skill. But, I shared all of this information with them, so that they could see that there is much more to crafts like this than what meets the eye.

Once my students had been prepped with the horrors of wallpaper work, I brought out some numbers. I kept it simple with easy fractions to work with.

We would charge one whole dollar per square foot for actually hanging up the wallpaper, ½ a dollar for taking down the old wallpaper (Once in a while rooms don’t have wallpaper to remove. Plus, you want to make this a separate price so that customers appreciate all of your hard work, and it doesn’t seem overpriced.), and ¼ of a dollar per square foot for prep work. (This would include cleaning the walls, caulking cracks, and spackling holes and other imperfections that the paper won’t hide.) These prices are from when I was first starting out. I actually did this kind of thing, regularly.

Next, I shared a simple floor plan with my students. Some of them recognized the blueprint for what it was. I showed them the illustration of doors and asked them what the rectangle representing a closet was. We discussed what was happening in the picture for a minute. And then, I told them that our customer wants to wallpaper the two bathrooms. 

The image was presented on an interactive Google Jamboard, so I could write on the board. I used a bright blue to rewrite the dimensions of the bathrooms in question. I told them that the ceilings were 8 feet high. When I turned around, I was met with incredulous faces. They had no idea what to do!

This was perfect, because it provided me an opportunity to teach. I told them that a good strategy when dealing with a difficult problem is to draw pictures. I drew four rectangles beside the image of the floor plan on the Jamboard. With a little prompting I got my fourth graders to figure out that we would need to find the square footage of the wall space that would be covered with wallpaper in order to create prices. “What are these four rectangles?” I asked. 

I’ll confess that the first time I did this lesson (I have an AM and a PM 4th grade math enrichment class) I tried drawing a three-dimensional image of the bathroom on the side of the floor plan, and this ended up being too difficult to understand. I ended up pulling each wall from my drawing out and making individual rectangle representations.

In my second attempt, I cut straight to the 4 walls. This was less confusing.

Either way, it required some spacial thinking to understand what to do with the numbers.
This was my first (AM) lesson.

Once it was established that my picture of 4 rectangles were in fact the walls, we labeled the dimensions: Each one was eight feet high, and two were one length, while the other two were a different length. 

In order to figure out the square footage of all of the walls, you solve the area of each, and add them together. This reads simple enough, but my students had never had to do anything like this before! 

It took a little convincing to show them why we needed the square footage at all. I used the dimensions of our classroom and kept it to only one surface; the floor.

“How big do you think our room is?” I prompted. After a couple of guesses, I told them that I thought it was about 30 by 15. I then paced out the floor and found it to be 11 paces by 6 paces. “If we calculate each pace to be worth 3 linear feet, what are the actual dimensions of the room?” Wait for it. My students knew to multiply 3 times 11 and 6, respectively.

“Are 30 and 15 easier to work with?” 

We used the dimensions of our classroom floor to practice. (The -100 was subtracting the cost of supplies.)

“They are compatible numbers,” Evie answered. I beamed with pride. We’ve been talking about using helpful numbers to do mental math a lot.

“That’s right; Much easier to work with. And, what is 30 times 15?” Blank stares. “What is three times 15?” Now we were thinking! When we figured out the answer to that, I wrote “15 X 3 X 10” on the Jamboard. “Thirty feels big, but pull it apart. It’s just 3 tens.” 

“So we know that the floor of the classroom is about 450 square feet. How much would it cost to wallpaper the floor… Of course no one would do this, but what would it cost?” Everyone quickly understood that it would cost $450, since each square foot would cost one dollar. 

“Now, let’s say that some maniac had already wallpapered the floor before we were asked to. What?! Crazy, I know, but what if… We would have to remove that old paper before we can apply any new paper. How much will that cost? It’s fifty cents per square foot,” I remind them. It doesn’t take long to figure out half of 450. 

“And, finally, there will be some prep work before actually wallpapering. That costs twenty-five cents per square foot.”

In order to illustrate this concept, I drew a square on a new, fresh Jamboard slide. I labeled it $1. Then I drew another square, the same size as the first, and drew a line down the middle. I labeled each half $.50. Before going any farther, my math enrichment students knew to halve the half. 

While a couple of kids knew what to do with the twenty five from $225, some didn’t. I told them to break apart the number. “Don’t think of it as 225. What is half of two hundred?” I wrote 100 on the board when they said it aloud. “What’s half of 25? How do you know that it’s 12 and a ½?” 

Evie-to-the-rescue-again explained that 24 divided by 2 is 12. The one extra that it takes to make it 25 can be split in half. “Nice,” I encouraged.

“So, how much would it cost to do the whole project on the floor of the classroom, provided some nut wanted to wallpaper a floor?” Staring students looked stunned. “You have the price for applying the wallpaper,” I said, circling the $450. “You have the price for removing the old wallpaper.” At that point, I circled the $225. “And, we just figured out that it would cost 112 and ½ of a dollar to prep the surface.” 

“Do we add it all up?” a hesitant student asked. 

“That’s right,” I said, trying to sound proud and hoping to steer my students toward feeling like they can do this. “Now, time to figure out what this bathroom would cost!”

I let them struggle a little before helping. They needed a bit of guidance. But, we figured out the square footage of all four walls. They did pretty good finding out what it would cost. And, the second bathroom was a little easier. 

A funny experience happened at the very end of the afternoon lesson. This PM group of fourth graders originally entered the room with the announcement that they already knew the answer to the problem.

A couple of them had walked in on me finishing up my morning math enrichment lesson. They confessed that they already knew the final answer to be $952, “or something.” 

I told them that I was going to change all of the numbers, so it will be different. They thought that sounded reasonable;)

I had intended to make the ceilings 9 feet tall for the PM class, but the concepts were difficult enough to understand that I didn’t feel like it was all that necessary. But, by the very end of the afternoon lesson, after I told the students to take the prices of the two bathrooms and add them together so that we can tell the customer how much it will cost… 

“Wait,” they exclaimed. “You didn’t change the numbers!” Huge smiles stretched across their faces. They loved being tricked.

“Look at that. You ended up needing to do all of the work, anyway.” We all laughed as they exited the room. 

Communicating Creative Mental Math Verbally

“I don’t know how I got it; I just know that this is the answer,” a frustrated student defends himself against the inquisition of an even more frustrated teacher who wants him to “SHOW YOUR WORK!”

You should have seen the students’ eyes bulge when I told them I was going to give them candy! LOL They were happy to gobble up the math, though.

But, what if he actually doesn’t know where the number came from? We don’t ask the toaster to “Show us how it heats up our bread.” When was the last time you insisted that the mechanic “Show you HOW they fixed your car”? (They always try to explain it to us, and I’m like, “Does it work? How much does it cost? I got stuff to do.” Ha ha;)

I recently had a math enrichment lesson with second graders where I told them what they didn’t know they did with a couple of mental math problems. We were working on comparing three-digit numbers. I had printed pictures of snacks that had prices on them. Teams of students were first asked to arrange the snacks in order from least to greatest price. Then I asked the class to compare the cost of three items to the cost of two others. The students didn’t have paper or anything to write on. 

Please pardon my penmanship;)

After I received some successful answers, I asked the teams, “What did you do in order to produce those answers?” I got a variety of responses. Most teams told me the names of the operations. “We added the three numbers together, and then subtracted…”

One group explained what they did to complete the operations, and I was very impressed. While students were sharing, I took some notes on the board. I clarified what the group was communicating by drawing circles around numbers and pulling out concepts.

“You began by adding 65 cents to 55 cents,” I reiterated. Nods of heads confirmed the accuracy of my statement. What happens in a creative mathematician’s head is a little different from what one would do on paper, however, and I wanted to pull this out. These students hadn’t used an algorithm.

I like to do a lot of mental math in my room, because it helps kids develop number sense. “The 65 and 55 are both pretty close to a number that is really easy to add in your heads,” I told them.

Here’s a post that shows 3rd graders communicating the use of compatible numbers to multiply.

“Fifty!” the group called out. We have been identifying compatible numbers, so they already knew to look for something more manageable.

“That’s right. And, in order to get to fifty, you have to adjust these a little.” I circled the 65 and wrote 15 on the side. Then I circled only the 5 from the ones of 55, and I wrote that near the 15.

If a student had paper in front of them, they might line up 65 and 55. Then they’d add the fives from the ones’ column and regroup with a “one” above the tens column… But, do we grown ups do this in the grocery store when we are comparing one item with another? No, we use mental math. We develop creative tricks that we may not even realize we use!

My aim is to unlock this mathematical creativity early in life. A secondary goal is to help students be able to communicate it.

“After adding the two 50s together, what did you do?” Everyone can see that there is still a 15 and a 5 written on the board. I wrote the sum before anyone called out, answering the rhetorical statement myself. “Now, you need to add this $1.20 to 99 cents. That sounds hard,” I teased, knowing that they’d already smashed that algorithm in their minds.

Letting students work in teams allows them more than just Social Emotional Learning (SEL). They help one another remember and recall sums and differences.

When I told them about using 100 instead of 99, several students silently shouted, “That’s what I did!” No one is going to carry a one from the tens to the hundreds column of a mentally constructed algorithm. And, we don’t always have paper. AND, do you really want to teach your students to be dependent on paper?!

Now, think about it, reader. Students are using subtraction in order to add numbers together. What 8 year old is going to be able to explain this abstract use of arithmetic in writing on a test or assessment?

Here, I’m having the group of 2nd graders “play” with numbers by lining their teams up in order of least to greatest, having constructed the largest number possible with the loose number cards I’d given everyone in each team. Get-up-and-move-around-math.

And, we (myself included) expect them to “Show their work!” I’m happy if they know what they are doing and get the correct answer. I’m nearly 50, and I only just learned how to show MY own work! LOL

What I found myself doing in the past was asking students who had performed mental gymnastics to achieve a remarkable mathematical feat to write down the steps they took. In other words, if you added up three numbers (65 + 55 + 99), and then subtracted a fourth from that sum, write it all down…

Even if you can’t describe the exact process of creating the sum or exactly what you did to subtract. Just tell me what you did with the numbers. I, like every other math teacher in the world, wanted to see more than just an answer!

I think that having students use mental math, and then having them explain what they did VERBALLY is helpful in sharing the mechanics of the creative math. It’s easier to verbalize than it is to write. I bet there are books written about this. (If you know of any, please share. Thank you.)

A tool I’ve enjoyed having students use to verbally communicate their creative math skills is Flip (formally known as Flipgrid). Kids can make videos of themselves talking about the math. They can also write on their screens to show what they did while talking about it. If they did the math on paper, they can take a photo of their work to include in their video. Finally, they can watch each other’s videos, get ideas for future creative math projects, and leave encouraging replies to each other. The platform is easy to navigate and teacher-friendly for leaving feedback and assessment info.

In conclusion, while I always instinctually knew that forcing a kid to write down everything they did in their head could squash their creativity, I never knew how to bridge the gap between teacher and student; The chasm between the answer (what the student produces) and the process (what the teacher cares most about) before now. I’d tried varying techniques with varying results. My new thing is to verbally walk them through tricks I’d use to do mental math. Through this process, they recognize some of what they are already doing in their minds. They are learning how to communicate it. And, some students are learning creative ways to play with numbers.

Math Games: Dessert for Dinner?

What if you could produce a dessert packed with protein and healthy nutrients; I’m talking even more beneficial than a typical meal. Would you serve this delectable dish for dinner every day? My conclusion may surprise you.

Last week was Parent-Teacher-conference-week at my school. Students had half-days, and families either visited the building or used virtual conferencing tools to converse face to face with educators. This was the very first time that I bounced around from teacher to teacher, visiting the conferences of my gifted students’ parents. While there are many ideas that I could comment on, the one that stands out most was from the parent of one of my math enrichment students. 

The family has a third grader who is gifted, and that is why I was attending the conference. But, his little sister, who is in first grade, attends my math enrichment lessons, and it was something that she said that got me thinking. Her parents told me that they asked their daughter what she did in math enrichment class, and she told them, “We play games.” 

“Is that all?” I imagine them pressing, being the good communicative parents they are. Yup, is the first-grade answer:) 

This is a recent pic of 2nd grade learning to play Dominos.

I laughed when I heard their tale. I explained to the parents that I was teaching the first graders Dominos. After defending the fact that there is a lot of mental math and problem-solving, there was some light banter between parents and the regular ed teacher about only knowing the stacking and tumbling side of Dominos. 

Because their gifted third grader had already experienced lessons showing the critical thinking development of Dominos, it wasn’t necessary to get too defensive. They were “on board” with my use of games for strengthening math skills. But, the idea of my lessons being categorized definitively as nothing more than games gave me pause. Initially, I was perfectly okay with tricking students into learning through having fun. What teacher would turn down that strategy? “Can we have some more math enrichment, please!” the students whine. “Um… Yes!” every math teacher in the world would utter. 

Then I thought about the idea of turning everything into a game. Wouldn’t that be wonderful for the students? But, would it be healthy? Hmm… 

This is where the thought experiment at the top of this blog originated. I was musing over my math lessons being perceived as games, and I dreamed up the analogy of only eating dessert. Prepare to enter a rabbit hole of research. I’ll try to keep it palatable😉

History of Dessert

Asking “Why does dessert even exist?” feels a little like questioning the purpose of gold or jewels. Isn’t it obvious? It’s awesome! 

Believe it or not, dessert did not always exist, however. Similarly to gold and jewelry, it was discovered, and has evolved over time. The French are responsible for turning entremets into dessert (Gerson, 2019). Before there were sweets to end a meal, entremets were served as “interval” dishes, literally “between-foods” courses (Teppen, 2015). They were meant to cleanse the palate. They may be sweet, but not necessarily. 

Eventually, a final course of fruit, called le fruit, was formalized (Gerson, 2019). Only, before serving it, the table must be completely cleared. This cleaning of the table was called desservir, the French verb for “to clear.” More than tasting wonderful, the original final course of fruit developed into something lovely to gaze upon. Some desserts even consisted of “Elegant metal and glass structures holding whole apples or plums. Other times, meticulously crafted sugar figures became the center of dessert displays, and might not be eaten at all. Dessert specialists in the eighteenth century were supposed to understand architectural design and be capable of replicating it in sugar paste” (Gerson, 2019). 

These creators of dessert, as it came to be known around the time of the French Revolution, when the Bourgeois assimilated the term, were originally more like artists than chefs. Maryann Teppen (2015) writes of an entire battle scene, complete with tiny sugary soldiers with guns and canons, that told the story of Louis XV’s demise crafted out of sugar. It is hard to imagine your dinner table being cleared; plates, napkins, silverware, and foods being “dessert-ed” away; only to be replaced by an elaborate, sugary scene of violence that you feast your eyes upon but don’t touch!

Modern dessert serves a different purpose. BreezeMaxWeb (2022) suggests it psychologically signals the end of eating. Consuming a small, sweet treat at the conclusion of a meal might communicate to the body and brain that we are all done, and there is no need to nibble superfluous snacks. The End. 

A practice that I began a couple of years ago has helped me lose some weight and become more healthy; I will eat an apple at the end of every lunch. Many years ago I heard that apples help clean your teeth, and apparently there is some truth to that (Apples: Dental Hygiene Facts, 2017). Once I’ve eaten my apple, I cannot/will not eat anything else. I don’t want to undo my teeth cleansing. This has helped me de-snack my afternoons.

Let me reintroduce the concept of math games, here. Could a game be used to transition from one course of subject matter to another? Would playing a game cleanse the cognitive palate, and prepare students for something completely different? Of course! Would this be an appropriate way to signify we are done with the subject? I think so.

Delayed Gratification (Deferred Satisfaction)

How many parents use dessert as a reward for finishing a well-balanced meal? That treat is the ribbon at the end of a race. Some contests require more work and take longer, but when getting to the game of a lesson is the goal, students may trudge longer, work harder, and persist through all kinds of problems. Those students who finish first might learn patience through having to wait for their peers to catch up with them before the whole group can consume the dessert of a lesson together. 

Self control. Training. Conditioning. “If I let you eat this piece of cake, do you promise to gobble up all of your peas and carrots without complaining?” doesn’t just sound silly. I probably don’t have to tell you that this is an ineffective reward model;) 

These are this year’s 3rd graders (math enrichment), learning the game, Cribbage.

But, what if the dessert is carrot cake? What if the dessert is healthier than the dinner? Then what? “Eat all of your cake, or you won’t be given any peas…” Wait, what?!

Is there something to be said for learning to crunch through cardboard in order to earn cake? According to a longitudinal study spanning 40 years (Casey et al., 2011), learning and practicing self control early on in life can lead to better academic performance, less behavior problems, and even higher SAT scores. Casey and company (2011) describe in their paper, “Behavioral and neural correlates of delay of gratification 40 years later,” some ways kids can curb the pull of stimuli by learning cognitive control. There are mental strategies and tricks that people can use to provide buffers, dampeners, and walls to contain and maintain self sovereignty. Students may never learn or develop these important skills if they are never asked to wait for anything.

Through reading this research I wondered if teachers, themselves, are bypassing the delay of gratification when they jump right into games to teach. What educator looks forward to grumblings from their students? I propose that most  would prefer praise of pupils happy with pedagogical practices over the squabbling of scholars required to earn a fun activity. Are we educators partaking in dessert before dinner when we teach with games?     

Dessert Before Dinner

Before we beat ourselves up too much, let’s bring our metaphor along with us as we explore a couple of Jamarillo’s fun list of 11 Reasons to Eat Dessert First (2023). This may initially seem like a self-serving exercise, justification, or defensive maneuver, but hold on. Jamarillo raises the point that food can sometimes be a serious psychological hangup. “When we have disordered eating, we can often develop food or meal fixation.  Dessert is one of the most common food items restricted. This can lead to binge restrict cycles and disruption of hunger cues” (2023). 

Is it possible for students to develop “learning disorders” by experiencing “binge-playing” with learning games after enduring unnecessarily long restrictions? Just as Jamarillo (2023) suggests that dessert-first-eating can help overcome eating disorders through stimulating hunger, tapping into nostalgic memories, practicing navigation of bodily needs versus wants, and learning to respect cravings, beginning a lesson with a learning game can help students who struggle academically to open up to pedagogy.  

One thing more, and this might be a great way to end this blog, Jamarillo (2023) ends her short article with the fact that dessert is an ambiguous course. It can be a sweet, but doesn’t have to be. Fresh, raw fruit could serve as dessert. Pies, pastries, a tiny chocolate or candy, sweetened veggies, and yes, of course cake can all constitute desserts, whether eaten at the beginning of a meal, middle, or end. 

In conclusion, my first grade student may imagine all she does is play games during math enrichment time, but this learning dessert is rich with problem-solving proteins, mental math nutrition, and healthy higher-order thinking! With the short amount of time I have with my students, I have to make my challenges tasty. And, I’m okay with that;)

Sources

BreezeMaxWeb. (2022). Why Is Dessert Important After Eating Food?. Casa Romana Sweets. https://casaromanasweets.com/why-is-dessert-important-after-eating-food/#:~:text=When%20you%20eat%20dessert%20after%20your%20meal%2C%20it%20signals%20to,moving%20after%20you%20eat%20it.  

Casey, B. J., Somerville, L. H., Gotlib, I. H., Ayduk, O., Franklin, N. T., Askren, M. K., Jonides, J., Berman, M. G., Wilson, N. L., Teslovich, T., Glover, G., Zayas, V., Mischel, W., & Shoda, Y. (2011). Behavioral and neural correlates of delay of gratification 40 years later. Proceedings of the National Academy of Sciences, 108(36), 14998–15003. https://www.pnas.org/doi/full/10.1073/pnas.1108561108 

Cherry, K. (2023, November 5). The Meaning of Delayed Gratification: Deferred Satisfaction and Its Rewards. Very Well MInd. https://www.verywellmind.com/delayed-gratification-why-wait-for-what-you-want-2795429 

Apples: Dental Hygiene Facts. Summit Dental Health. (2017). https://summitdentalhealth.net/apples-dental-hygiene-facts/  

Gershon, Li. (2019, August 21). The Invention of Dessert. JSTOR Daily. https://daily.jstor.org/the-invention-of-dessert/  

Jaramillo, S. (2023). 11 Reasons to Eat Dessert First. Peace and Nutrition. https://peaceandnutrition.com/11-reasons-to-eat-dessert-first/  

Miller, K. (2019, December 30). What Is Delayed Gratification? 5 Examples & Definition. Positive Psychology. https://positivepsychology.com/delayed-gratification/  Tebben, M. (2015). Seeing and Tasting: The Evolution of Dessert in French Gastronomy. Gastronomica, 15(2), 10–25. https://doi.org/10.1525/gfc.2015.15.2.10

Enriching Extension Activities: Grinch Escape Room

Ready Math has an enrichment activity for nearly every math lesson. These are usually accompanied by a worksheet. The papers can be printed, photocopied, and distributed for students to complete during independent time. The worksheets have thorough instructions on them, sometimes with examples, so that students can manage the assignment without teacher help. 

In the “Teacher Toolbox” you can find an array of tools for each lesson for every grade. I like to start off with checking out the “Extend” ideas and adapt them to meet my students’ needs.

The idea is for students who’ve attained mastery of the subject to apply their skills to slightly more challenging tasks. It’s nice for the teacher to have something concrete to look at after the student is done. This evidence of work and proof of advanced mastery can be shown to parents and back up grades on report cards. 

One problem with this is that students aren’t always thrilled about being rewarded with a worksheet when they understand and are good at a math concept. It’s helpful for a teacher to introduce the worksheet. They can spice up the assignment with some extra enthusiasm. It might be helpful to pave the way for success with a check for understanding of the assignment. Perhaps the teacher could introduce a twist to the pre-made project, including an additional step or task.

When I am preparing an enrichment activity, I try to provide an opportunity to use the math concept in a real world scenario. We all remember the age-old question, “When will I ever see this in real life?” uttered with a groan and eye-rolls. This is my aim: Show students situations where their math lesson would actually be found. 

Another goal of mine is to help students grow their thinking muscles. Perhaps there isn’t a clear use of Pythagorean’s theorem in everyday life, but it can be used to sharpen geometric and algebraic understanding! Puzzles are great for this. 

I recently used one of Ready Math’s enrichment assignments to challenge a group of fifth grade students. The lesson/worksheet looked a little like busy work; It involved adding and subtracting four-digit numbers with decimals. You needed to be handy with the math to complete the task with accuracy, but I didn’t see any way that the student would be richer having completed the assignment. 

One of the first things I do when attempting to turn a pre-made assignment into an enrichment activity is see if there is some bit of information or number that can be taken away. Can I remove something, and the students still figure out the answer? 

The assignment that I was looking at was a three by three grid with some boxes filled in and others blank. Every row and column, as well as the diagonal lines crossing the center square, all add up to the same number. The worksheet tells the students what the shared sum is. Can I remove that final answer and students still figure out what numbers would go in the boxes? 

I tried it out in my journal. The way I saw it, there’s no way around having at least two unknowns. I could ask the students to figure out multiple correct answers; sums of every row and column, but this kind of activity stretches beyond enrichment and requires gifted thinking. That is a topic for another blog; the difference between enriching math and providing gifted instruction. 

I tried playing around with the numbers in my journal.

Still liking the idea of removing the sum that all of the numbers share, and making students really dig for the gold of their lesson, I decided to limit the unknowns by providing parameters. I began writing these into hints or clues. Then, the lesson morphed into a type of riddle. I left gaps in the clues, so that students would have to address a few empty boxes in order to solve the entire grid.

As the project evolved, it struck me that I could pretend the problem was a lock that prohibited the class from leaving the room; It facilitated an escape room sensation. This would be the way that I presented the whole problem! I’ve been wanting to explore the use of escape rooms at school. This could be a great start. 

I prepared some more clues for bits and pieces of the four digit numbers within the grid. I put an image of the grid into a Google Jamboard. Then, I copied the riddles and pasted them into “sticky notes” that got spread out around the grid. I themed the whole thing with Grinch, and it was ready for “production.” 

The fifth graders loved it. When I told them that they were stuck inside the Grinch’s lair, their faces lit up! “The Grinch, that big ole meany went and scribbled over the sum that we need to solve this grid. He left us several riddles to figure it out. You can’t leave the room until you do.”

Everything was going great… Until… One of the students had actually completed this particular worksheet in the classroom, as an extension activity. My heart instantly sank. Did the Grinch steal my Christmas? Luckily, I’m pretty good on my feet, and I told them that we can still use this whole activity in order to learn how to make up our own riddles and clues, so that we could develop another, future escape room that other students could have to solve. Everyone was cool with this new plan.

I wrote an equation on the board, using as much information as was available. Then we filled in missing pieces with information from the clues. I showed them how they could do this on their own in the future! It was still fun.

We continued exploring the clues, now with a new purpose. Granted, we were working backward, since we already knew the final answer, but that was okay because the students were able to see how the clues functioned. I showed them the way you can start with an answer, analyze the number’s attributes, and make up hints that color and shade the number, without giving it away. They seemed to like it, and we still had to do some adding and subtracting of four digit numbers containing decimal points! 

This lesson wasn’t over when this group of students left, however. The way fifth grade math enrichment works in my school, I meet with a different group of advanced math mastery fifth grade students in afternoon. I told the AM students to not tell the afternoon math students the answer, just in case none of them had completed this particular assignment. Then the Grinch let them out;) 

Between the groups, my fourth grade gifted students painted a giant Grinch face to hang up over the door. That was fun.

When the afternoon students entered the room, I pitched the escape from the Grinch’s Lair idea the same way I had with the morning crew, but with the understanding that they may already know the answer, like the first group. One student of the eight or so kids had done this assignment and knew the answer, but he was a good sport about keeping it a secret. 

Since I had thoroughly examined the entire riddle with the first group, I was well-versed in the clues and could easily present them to this final class. I let them wrestle with the ideas. As it turned out, you could figure out the final answer before getting all the way through the final clue. That was interesting to learn. The experience was pretty fun, and they got plenty of practice adding and subtracting numbers containing decimals. 

I’m definitely looking forward to making more lessons containing clues and using the escape room scenario to encourage tension and motivation! It was really nice to have a pre-made template from Ready Math to build from; or, more accurately take away from. But, in the future, I’ll have to be careful about assuming kids hadn’t used the lesson before. 

Multiple Enrichment Opportunities: Multiplication and Compatible Numbers with 3rd Graders

The idea underlying math enrichment is to deepen the understanding of math concepts that advanced students have already mastered. I began meeting with the top math students from each grade level (K-5) a few weeks ago, and I started off my introductions with this definition of enrichment. I didn’t want them to expect to go farther in their math skills, surpassing their peers. I also didn’t want them thinking that they were “above” their classmates who did not join me for this enrichment time. Rather than looking down from the mountain tops, we would dig in; We are in search of the riches (from en-rich-ment) that can only be found by looking beyond the ordinary teaching of math skills.

The challenge to myself is to find novel ways to show the use of math skills. I want the students to see that what they learn in the classroom is very necessary. Even if you never, ever have to use Pathagoream’s theorem, being able to use a formula correctly and understanding why is extremely valuable. 

An example of this is my lesson on multiplication for 3rd graders. Having completed an “Understanding Multiplication” lesson weeks earlier, and learning facts for multiplying zero through ten, I wanted to have students use these ideas creatively. I came up with a lesson that shows a way adults use multiplication all of the time without even realizing it!

There are four 3rd grade classes. Each one is very close to 25 students. How many students are in 3rd grade? Adults immediately know that there are about 100 kids in the 3rd grade. How? We instantly know that 4 X 25 = 100. Easy-peezy. But, there are a few things going on behind the scenes. We, grownups, are already rich in the knowledge of four 25s equaling 100, due to decades of dollars and quarters! Also, we know to use the compatible number 25 when numbers are close to it. Third graders have been taught how to round, but they don’t know that it is okay to completely change numbers into “easy to use integers” (compatible) for simplifying computations!

I told them that they could simply add all of the numbers together, first. That way they know what they are aiming for. But, they have to show the use of multiplication to complete the problem.

As always, I wasn’t going to just come out and tell them all of this. My math enrichment students had to dig for it, en-rich-ing themselves. I gave them this math problem. 

It has to do with them, which is fun. The numbers are accurate. I looked them up on the school’s database. These are the names of the actual third grade teachers. 

I read the problem to the enrichment students. Then, I asked them, “What is this problem about?” After the students identified the topic of third-grade population, we discussed what the goal was. You have to provide the total number of students, but there’s a catch; “You have to use multiplication to do it!”

When I walked the students through the Important Information; the data that will be used to solve the problem; I paused to point out some key elements. The students noticed the multiple 26s. I showed them that there was something else they all had in common; They were all in the twenties. There were multiple numbers with a two in the tens. 

Finally, it was time for the students to do their work. “Dig in!” I had put the word problem into a Google Jamboard, so I could make a copy for each student in the Google classroom that I’d shared with the enrichment students. They were able to write on the Jamboard, using their iPads. I walked around and witnessed the digging. It was awesome to see the variety of computations. When students told me that they were done, I showed them how to duplicate the Jamboard slide, erase their math, leaving the word problem, so that they had a new work space to solve the problem in a new way. 

After letting the students wrestle with the word problem for several minutes, I had students share their calculations. One student multiplied the totals of class sizes by 1 before adding them all together. “Does this meet the parameters of the problem?” I asked the class. Yes. “Is this useful, though?” No. The student had only done this after I told them to come up with multiple ways to solve the problem. I was glad they had, because it was an opportunity to point out making math work for you. “Multiplication is a way to simplify math, believe it or not,” I told them. “Can you multiply 20 times 4 in your head?” Yes; see? I reviewed with the group that multiplying anything times 1 is the identification principle. It simply tells you what you are working with; “One times Dominic, means you have one Dominic” 😉

I had students share their Jamboards on the classroom Googlel Jamboard, so we could witness the different ways to use multiplication. I was impressed by a few students breaking apart bigger numbers before multiplying. Only a couple of students recognized the closeness of the class sizes to the number 25. This presented a teachable moment, and I shared the vocabulary/math concept of compatible numbers. 

After this, our time was up. I mentioned that time, like money, presents some compatible numbers. “What is 4 times 15?” I asked the class. When no one answered immediately, I asked, “How many fifteens are in an hour?” They knew this to be four. “So… four 15s makes up one hour… ?” 

Sighs and “ah has” could be heard. “If you have a few numbers that are near fifteen, could you use fifteen as a compatible number for multiplication?” Hmmm… 

Average Salt Consumption: 5th Grade Math Enrichment

In the excitement of beginning a 5th grade math enrichment club I created a math problem that may have been a bit extreme. I wanted to use something from real life, make it challenging, and leave my students thinking. 

Photo by Castorly Stock on Pexels.com

The topic I settled on was sodium; specifically, our salt intake. What 5th grader can resist paying attention to a life and death lesson? They may have already heard about salt consumption severity, but if not, they will! This should make the lesson stick. (see “Explanation” of The Power of Contrast.) As it turned out, I was right. Not only did a few of the 5th graders understand the dangers of salt, but some knew that too much can negatively affect your blood pressure. 

In order to increase the cool-factor of the lesson, I explained the importance of salt in conducting electricity throughout your body. I did this by asking them which is more dangerous during a lightning storm, swimming in a chlorinated pool or a salt water pool. Salt is a much better conductor of electricity than regular, clean water. They were energized by this new information. (For a very easy to read article about salt’s necessary functions in our bodies, check out “Pass the Salt: Sodium’s Role in Nerve Signaling and Stress on Blood Vessels” by Abbey Bigler-Coyne. And, here is an awesome, short read about salt’s dangerous properties during lightning storms: “Ask the Physicists: Swimming in a Lightning Storm“)

I knew that the 5th graders had been working with decimals. I thought it would be fun to make a problem that had them wrestle with decimals in more than one way. We would average our salt intake. 

First, I did some research. According to the American Heart Association, humans would ideally consume 1,500 milligrams (or less) of salt per day. Written in decimal form, this translates to 1.15 g.

American foods are loaded with salt, and our favorites are the worst! For lack of time, I did not burden my math enrichment students with too much detail. They had no trouble understanding what foods are super salty. They mentioned French fries, hot dogs, and chicken fingers. Then, we discussed foods that didn’t seem salty, but definitely had some, like ice cream. 

This set me up for presenting my word problem: While the human body needs some salt (only around 500 mg), too much of it can be harmful. It is recommended to consume around ½ of a teaspoon or less per day. A half of a teaspoon of regular table salt measures about 1.15 grams. 

Some foods are notoriously more salty than others. In the interest of being healthy, one might try to consume less salt on days surrounding heavy intake periods. 

Look at the data to the right. How many days will this person need to consume only 1 gram of salt in order to bring their average down to 1.15 grams per day?

How It Works

Before going over the problems with my 5th grade math enrichment students, I taught what it means to find the average of a few numbers. I pretended that the students had taken a quiz, and I wrote some fake scores on the board. What was the average score? It isn’t necessarily the middle of the range (distance from smallest to greatest). I had written 10, 8, 5, 6, 8, 4, 0. (They insisted that someone get a zero; Rude! I suggested that the zero was probably due to the person failing to put their name on the quiz, and couldn’t get any credit;) 

There were two 8s. That might pull the average up. “You use an algorithm to find the average, and it can adjust,” I explained. I showed them how you add all of the numbers together, and then divide by the number of scores. “There’s more than one 8, so that should cause the average to weigh heavier on the higher end of scores. But, then the zero is going to drag the average down.” 

“It is like tug of war,” I explained. “The higher the scores, the more the rope gets pulled in that direction. If there are more low scores, the rope begins to go to that side.” 

We played with the numbers, changing them a few times. I showed how, when you raise a few grades, the average goes up. I had students make predictions. 

Next, I showed the 5th grade math enrichment team our word problem for the day. I read it to them, and then asked them our Ready Math questions that help us understand word problems:

  1. What is this problem about? A. Salt; Adjusting the average consumption.
  2. What are we asked to find? A. The number of days necessary to significantly decrease our average amount of salt consumption.
  3. What is the important information? A. The amounts of salt we consumed over the weekend, our goal, and the amount of salt we will allow ourselves to eat until we reach our average goal.
  4. And finally, what are you going to do? A. Continue figuring out the average of the three weekend amounts, combined with ones (1 gram per day) until you reach an average < 1.15 g.

They understood the story of the problem. We ate way too much salt over the weekend. Now, we feel the need to eat extra healthy to make up for it. 

I walked the class through one or two tries: “If you consume only one gram of salt during the day after the weekend, what happens to the average?” We added up the number of grams, and then divided by the four days in question. 9.61 ÷ 4 = 2.40, still too high.

I had placed the word problem in a Jamboard. When I pushed the lesson out to my 5th graders via their new 5th Grade Math Enrichment Google classroom, I made a copy for each. I let them wrestle with the numbers on their own for a few minutes. I showed them how you can “duplicate” a slide in Jamboard, so that all of the important numbers and word problem get carried over to another clean workspace. I wanted them to try the math a few times, showing me their work. 

I caught a few of them trying to average the three days of the weekend. I told them that this was unnecessary, because we already know that every single day of the weekend was way over our end goal of 1.15 g! “You can go ahead and practice averaging, but this won’t get you to our goal: Finding the day we don’t have to limit our salt intake to only 1 gram.” 

After a while, I wrote the weekend numbers on the dry erase board: 2.56, 3.08, and 2.97. Then I said, “What if you eat only one gram of salt for the next ten days?” I drew ten ones next to the first three numbers. “In order to find the average, you first add all of the numbers together.” I drew plus symbols between every number. “Next, you divide by the number of weights.” I walked them through dividing 18.61 by 13. “The average intake would be 1.43 grams per day. This is still too high, so we have to continue eating only one gram per day a little longer.”

We hadn’t found the answer by the end of our time together, but that was okay. This time of math enrichment was meant to provide teaching that they can bring back to class and use on their own during independent work time. I had hoped that some of the students would continue working on their salt word problem throughout the week, when they finish their other work. 

A few students seemed excited about finding the accurate number of days as they left the classroom. They told me their tries and expressed surprise at not finding the answer yet. I told them to keep going. It was out there!

I found out later that a few students expressed to their math teacher that the problem was a little too hard. This inspired me to include the next part of this blog; The explanation. 

I chose 1 gram to be the new amount that the person consumes each day because you could eliminate one of the steps from the algorithm for solving averages, if you used increments of ten days. More than erase the step, you do it mentally. We already did ten days in class. That wasn’t low enough. Next, try 20 days. If you remember that the three days from the weekend is 8.61 g, all you have to do is stick a two in front of it! Then put a two in the tens place of the number you are dividing by; 23 (twenty more days + the three weekend days). At this point, it would be best to use a calculator to figure out the long division. (I never said that you couldn’t. I modeled using long division, but once you leave the classroom… 😉 Just show your work!! Write down what you did. Document each try, the answer you got, what you did. Be a scientist about it. 

Once you find between what two tens your answer falls, you can begin narrowing your work further. 28.61 ÷ 23 = 1.24 (twenty days of 1 gram of salt per day); 38.61 ÷ 33 = 1.17 average grams of salt per day; close, but not there yet; 48.61 ÷ 43 = 1.13 We made it! …But, we only ate one gram of salt for more days than necessary. We overshot our goal. In order to figure out the exact day, we could go back one or two days at a time. Maybe try the middle; 35 days. 

One student messaged me within the 5th Grade Math Enrichment Google classroom, seeking clarification. She had taken notes on my example of ten days, and couldn’t remember why we added the ten to 8.61. I messaged her back, and a couple of days later, she had it! This student not only figured out the answer, but showed me all of her work. It is beautiful and impressive. 

In addition to this incredible success, however, I am pleased to share that some of the students were still mentioning the problem to me in the hall, days later. A student whom I see riding his bike when I monitor the crosswalk in the mornings queried if anyone had solved the problem, and we talked about possible solutions. I told him that it was more than 30 days. He couldn’t believe it. 

Congratulations to this amazing student! She did it. Great job!

Math With Chess

“How many more squares is White attacking than Black?”

This problem was awesome on a few fronts. Students had deciphered a Morse code message that shared a short sequence of chess moves written in algebraic notation. They played out those moves and discovered that one player had a huge advantage over the other. “How much of an advantage? Be specific. Can you put a numeric value to the advantage?” 

It all began with my preparing a lesson for chess club. I was going to teach club members about gambits. I researched the more common gambits and landed on the Smith Morra Gambit. I found a succinct video on Youtube that explained the gambit. While watching the video, I wrote down the algebraic notation. 

But, I wouldn’t just give them the chess code to learn the gambit; I decided to have my gifted students decode the code! My fifth grade gifted students were the first ones to see the code. They had only dabbled with decoding Morse messages. 

I had used Morse Code Translator to change the chess play sequence into dots and dashes. Rather than writing the number of the move; This was going to be confusing enough as it was; I decided to change the colors of the moves. White’s moves were turned to white dashes and dots. I made the background of the text box green, so that you could easily see the white and black codes. I put an image of my code, along with the Morse Code alphabet and accompanying numbers onto a Google Jamboard. The fifth grade gifted students were on it the moment they walked through the door. 

The two things that I shared with the fifth graders was that the slanted line (/) separates the words; In this case it broke up the moves, but I did not explain that. I told them nothing about the actual message. The second thing that I pointed out was where each letter or number’s code ended. The translator that I use makes it much easier and faster to produce Morse Code, but sometimes it is difficult to locate the space between each letter/number. After pointing out these two key factors, I stepped back and watched the struggle. 

Right away I heard a couple students divvy up the White and Black “words.” I was glad to hear the idea of collaboration. I wondered how long it would take for someone to understand that these were not actually words. The very first coded move was e4, the most popular opening move in all of chess. I heard a few people verbalize bafflement, but several recognized the move, “It’s chess!” someone shouted. 

I didn’t help them with any of it. At least one student knew enough to be able to read most of the algebraic notation and make sense of the moves. Of course I had a chess board and pieces handy, and we set up a game. I let the students figure out the sequence of play. When they came to the gambit on the second White move, I stopped them to explain what a gambit was. This was good practice for my chess club lesson that afternoon. A couple kids would get a double lesson, but that was okay. They could be my co-teachers! 

“The word gambit is closely related to gamble. It means taking a risk. A chess gambit happens when one player offers up a peace as a sacrifice in order to draw an opponent into a trap or sequence of moves that would benefit the aggressor (the one offering the gambit). Do you capture the sacrifice or risk the piece taking your own?” 

I had the fifth graders play through the short sequence until Black’s pawn was captured. Black had accepted the gambit, capturing the initial White pawn placed on d4. White offered up another pawn on c3. When Black captured that, White might feel a little on edge, because now there is a Black piece threatening the second rank of the White team! It is so close to attacking the Queen!! 

Before any more damage can be done, White captures with the Queen-side Knight, Nxc3. White has lost two pawns, while Black is only down one. If you were to only count points, it would appear that Black has the advantage, being up a point. A mere glance at the board should show even a novice player that White is in a much better position!

I explained to the fifth grade gifted students that the best thing to do at the beginning of a game of chess is to control the middle of the board. With that criteria, everyone can easily see the trap that Black has fallen into. There is a White pawn left sitting on the initial e4 square. And, now a Knight is “developed,” backing up the e4 pawn and attacking four more squares (b5 and d5 as well as a4 and e2).

The fifth grade lesson stopped there, but my fourth grade gifted students got a treat. It only took seconds for them to figure out that the Morse Code message was algebraic notation for a chess game. When I heard some groans, I told them, “The first to solve the riddle can play me in a game of chess.” Now, the heat was on. I set the board back up in the middle of a table while my students grappled over letters and numbers seemingly unrelated to one another. 

We worked through the Smith Morra Gambit sequence the same way I had with fifth graders. I had the fourth graders figure out the algebraic messaging. They figured out that the Xs meant a piece had been captured. I had to explain that the “d” in dxc3 meant that the capturing pawn had come from the d file. After explaining gambits and discussing the advantages and disadvantages of the board we were left with, I played a blitz round of chess against a pair of students.

Third grade was next, and these students are not only classy, but they are some of the hardest workers I’ve witnessed. Their grit knows no end. I presented them with the same problem. They labored through decoding my Morse Code message. We played the sequence out. I taught them what a gambit was, and we discovered the significant advantage that White was left with. But… Then I was hit with a question that I liked so much that I recorded it on video so that I would remember it: “We know that White has the advantage, but how much of an advantage? Can we put a number to it? How many more squares is White attacking than Black?” 

Not all of my third graders know how to play chess. I taught the team how each piece attacks. “How many squares is the King attacking?” I asked. I showed them how it moves. The answer was two squares. “How many squares are the Bishops attacking?” We looked at their lines of attack. I showed them the squares that the Queen attacked, including the Black pawn on d7. We went over how a pawn attacks diagonally and the way a  Knight moves. Then I set them loose.

A few floundered, so I guided them to make a T chart. “Let’s do one color at a time,” I suggested. “Also, how about we focus on only one piece?” We carefully counted all of the squares that the Black pawns were attacking (12). Then we counted up the Knights’ attacks (4).

Next we moved on to White. There was an empty square next to the White Rook, so that counted as an attacked square. We continued counting until we covered every piece. I missed a couple of the the Knight’s attacks, but Gray got my back. She caught my mistake, and we corrected the calculation.

In the end, we discovered that White was attacking 43 squares to Black’s 16, way more than twice as many! So, was the gambit worth it? I’d say so. And, what could Black do differently to limit the massive advantage? Don’t fall for it. Don’t take the gambit. Push forward or ignore, but definitely think ahead.

Worm Burning: A Mental Math Game

John Burger, second grade teacher extraordinaire (2012)

When I first began teaching, I had a mentor who was amazing. He taught second grade, and it was a calling more than a career. His name was John Burger. Rather than do Social Emotional Learning (SEL) lessons, he was SEL. Everything he taught had emotional and social lessons woven throughout it. Like myself, education was a second career for John. He had been an engineer before becoming a primary school teacher. More than the money, he was doing this because he believed in it.

In addition to John’s unique way of teaching, he used some teaching tools that I liked so much that I adapted them into my own repertoire. One was readers theaters. I have shared a few blogs about those in the past. Another was mental math games. 

The mental math games were designed to make math fun and exciting. They are a great tool to use on the fly, because students don’t use paper or pencils. They should do it all in their head. Some of the games require critical thinking. Some rely on short-term memory and problem-solving. Others practice rote memory math facts. 

One of my favorites comes with a story. John liked baseball, and each year, when he introduced this game to his second graders, he would tell them, “When a baseball is hit really hard, and instead of it going up into the air, it is a line drive, straight over the grass… If a worm were to stick his head up out of his hole just at that moment, it would get its head burned by that cruising missile of a baseball! This is called worm burning.” There would be all kinds of gasps as kids pictured a worm being scalped by a wizzing baseball. Then, in his soft, understanding style of sharing, John would explain how the game works. “I’m going to say a bunch of numbers, and I will tell you what to do with them in between. You have to try your best to keep up. I’ll go slow in the beginning, but then I will begin to speed things up. When I stop, you tell me the answer that’s in your head.”

“You have to keep the answer at the front of your brain.” Sometimes I lose it and have to stop.

The mental math game is fast. The teacher will use single digit numbers and a variety of operations, keeping track of the answer until the worm burner has run its course. When the teacher stops saying numbers and operations, students have to raise their hands with whatever answer they are left with. I have my students show me their answers with fingers; They raise the number of fingers that they think is the answer. The teacher (or student; I’ll have kids try it when they get good at it) who is sharing the math must keep the final answer under 10. 

I often teach students this game at the beginning of the year and use it during whole-group bathroom breaks or times I need to keep students quiet. We get really excited when we know the answer and/or get it right, so it is hard to be completely silent. I remind students that they ought to only raise the accurate number of fingers. I praise students who do this well. 

You change up the difficulty of the digits and speed by which you say them to adjust so that more students can participate. The students who are more fluent with their facts are affirmed as math whizzes, and that’s just the way it is. “Good for them. The rest of you can study and memorize your facts just the same.” I have witnessed students work on learning their facts and gradually move up the ranks in Worm Burning, until they became competitive with the best of the burners.

I usually try to do a few that everyone and anyone can get. You can weave in a couple of tricks, like multiplying the whole thing by zero. Then everyone gets in on the answer. It gets everyone to at least pay attention and listen. Also, the Polite Pirates perk right up when they hear me say, “subtract 99 or 98” because they know the going answer before that was probably 100, and we are back to only 1 or 2, respectfully. I’ve had lost souls jump back into the game at that point. It’s fun to see them grab ahold of confidence as they celebrate success.

Sometimes, but not always, I will go back and walk the class through the Worm Burn. I’ll demonstrate keeping the answer right there at the front of your mind. Often, the Worm Burn is so fast or long that I can’t remember all of the steps. The successful students are usually proud to help me remember, though.

Math Enrichment

Photo by Pixabay on Pexels.com

Later on in the year I will introduce larger numbers that can be tricky. For example, I will have students multiply 25 by 4. “I don’t know that!” they’ll cry out. 

“How many quarters are in a dollar?” I’ll ask them. 

“Oh…” They get it, and then I will do a bunch of worm burners incorporating twenty-fives. 

Photo by EVG Kowalievska on Pexels.com

Another number I’ll throw in at some point is fifteen. “Three fifteens is the same thing as three quarters past the hour. How many minutes is that?” I’ll explain after stumping my students. Sometimes I’ll use alternative words like “dozen” or “double that” to keep things interesting.

By the end of third grade I would be throwing fractions into the mix. It’s a great way to cement the understanding of denominators dividing numerators. I will get the Worm Burn to the number 24, and then say, “What is a third of that?” Or, maybe I’ll start off with “Three fifths of fifteen (9), plus three quarters of four (3), divided by six…” and so on. Pause just enough so some students can get it, but not so much that others blurt out the answer. And, don’t make it so hard that no one gets it!

Gifted

This year I have transitioned from being strictly a third grade teacher to the gifted support teacher for kindergarten through fifth grade of my school. I was sharing the game of Worm Burning with my third grade gifted students, when I saw an opportunity to bring the math to the next level… and then some.

I never write the Worm Burn on the board. But I foresaw a unique teaching opportunity here.

I told my third graders about a trick that I often use in order to keep the numbers straight and maintain a going answer in my mind; I will use the answer in the next operation. For example, “Two times three, plus six…” I added the six to reinforce in my own mind that the product of two and three was six. I never write the Worm Burn on the board, but in going back to show this trick further, I wrote out the sequence of operations from a previous Worm Burn. This introduced the idea of squaring a number, which then lead to teaching exponents.

Then I thought about how different Worm Burning was from using Order of Operations. And, out comes PEMDAS! We were already talking about exponents!

I started out with a simple Worm Burn, “One plus three, divided by two, times seven, minus four, divided by five, plus one…” The answer is three. I wrote the burn on a Google Jamboard and showed the sequence of math. Then I told my students that if I were to do this math properly, the answer would be completely different. They were intrigued. “What do you mean, properly?” they wondered. I wrote the acronym PEMDAS on the board.

When we followed the rules for order of operations, our answer was much more complicated. With the help of Siri, we were able to divide numbers that didn’t have obvious answers. How do you divide three by fourteen? Is that even possible? Well, if you have three boxes of cereal, can fourteen people have some? How much of all of the cereal would each person get? Ask Siri.

The final answer came out to -.5858, which was really weird. They were unfamiliar with decimal points, let alone negatives. It was an eye-opening adventure.

From Worm Burning to diving down a rabbit hole of increasingly complex math concepts, my gifted third graders were happy to transition to reading about everyone’s favorite vampire rabbit, “Bunnicula,” and take a break from arithmetic.