Tag: Enrichment

Buttery Batch of Math Cookies

This is the introduction that I used on my fifth graders.

In preparation for teaching a math enrichment lesson to my fifth graders, I looked at the iReady “Extension” activities in the Ready Math “Teacher Toolbox,” and I found a problem that I liked a lot. (iReady and Ready Math are products of Curriculum Associates. My district has been using it for several years, and I like it a lot.) This lesson (14) is all about using fractions to solve word problems.

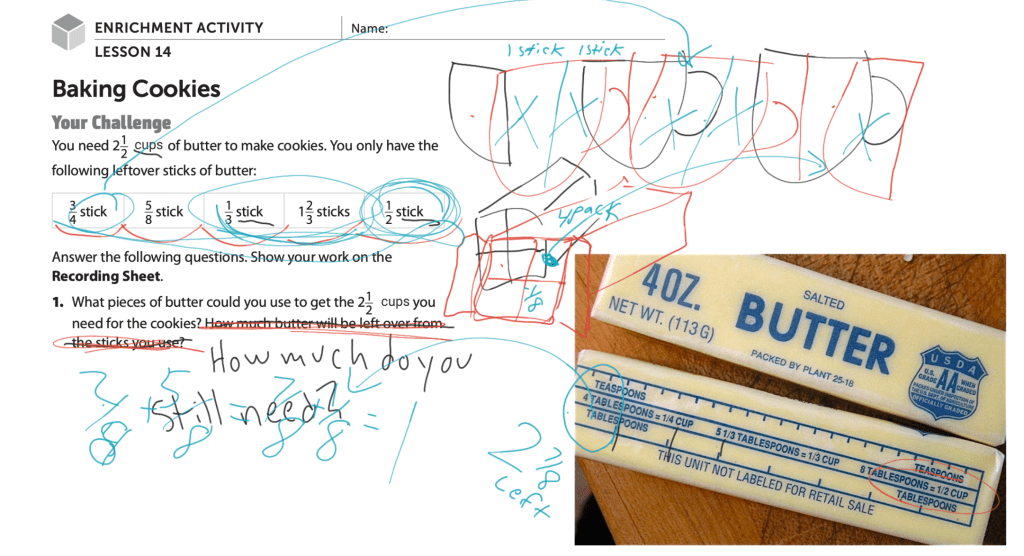
Here’s an image of the worksheet that a teacher could photocopy or share via Google classroom. Because I have the luxury of actually teaching enrichment lessons, I decided to do some explaining before handing over the problem. Also, I opted to make a few tweaks, too. In my experience recipes usually call for specific measurements of butter, not a number of “sticks.” Therefore, I covered up the word sticks in the problem and wrote in “cups.”

This changed the outcome of the answer quite a lot. Now, students would not have enough butter to complete the recipe. They could access new sticks of butter, but if they did that, then solving the problem wouldn’t require wrestling with all of the fractions presented in the partial sticks. That’s when I imagined the real-life experience of baking cookies after having worked all day at making a big meal, like Thanksgiving.

Needing soft butter for recipes is a real thing. Also, who doesn’t love consolidating? We can clean up all of those partial sticks of butter and make cookies at the same time!

I shared what a typical day of cooking in preparation for a large Thanksgiving meal looks like at my home with my fifth grade students, setting the stage for having several fractions of sticks hanging around. With the instruction to use up the warm butter first, and then dip into the cold butter from the new package, I set my students loose to calculate how much butter would be left.

Many students jumped on adding up all of the fractions. They began figuring out compatible denominators, so that they could combine every partial stick and find out what they had in all. “But, do you have to do that?” I asked them. No one wanted to venture a guess.

“What are you asked to find?” I pressed.

“Two and half cups of butter,” someone accurately answered. Without saying anything, I drew two of the worst cups ever drawn on an interactive board, followed by half of a third. I made fun of my drawings, which everyone helped with, pitching in their own digs. Once that settled down, I pointed out the lines I’d drawn through the middle of each measuring cup.

“Why’d I do that?” Earlier, we had discussed that fact that one entire stick of butter was the equivalent of half a cup. The students understood better than they could put it into words, so I articulated the concept for them, “Each half of a cup was one stick of butter.”

Then, we looked back at the fractions. It was easy to see that 1 2/3 + 1/3 would be able to fill one whole measuring cup. That leaves us with three fractions with differing denominators. “Before working out a common denominator to add up all three, think about what you are trying to do,” I instructed. “What is your aim?”

I showed the students that 1/2 a stick of butter + two of the 3/4 would equal one whole. “That would take care of half of a measuring cup,” I told them. Also, I should mention that I crossed out halves of measuring cups, as we discovered combinations of partial sticks of butter that would fill them.

“If we used up two of the quarters to combine with the 1/2 a stick and create a whole stick, how many quarters are left?” One quarter. “And then, we have 5/8 of different stick left.”

They instantly got it. We were 1/8 short of a whole stick of butter. In the end we needed one whole cold stick of butter, plus 1/8 of an additional stick to add to all of our warm butter fragmented sticks to fill our two and a half measuring cups.

The Ready Math extension lesson (14) has a second question that I left as is. The catch is that my students used our additional left over cold butter (2 7/8 sticks) from my adapted first problem to solve it. I let them struggle with this one for a few minutes before I showed them the short cut of drawing pictures.

“You might think it childish to draw pictures,” I began. Fifth grade is the oldest grade in my school, so these were the seniors of the place. “…But, I find it easier to manage some problems when I sketch what is happening.” I had been watching them crunching numbers, making common denominators again, and subtracting fractions. Now, within a handful of seconds, I showed them how many quarters could be made from two sticks of butter! I pointed out the idea of labeling the quarters in order to keep track of my thinking. I wrote a B above each “batch” of cookies. Sure, I could just count the quarters, but when it came to the last stick, it will be important to identify what portions of butter will complete a batch.

As I divided the last rectangle into eighths, I asked, “What am I doing to this last stick of butter?”

Rather than answering my question, they were chomping at the bit to be the first to spew the solution to the problem. “Eleven and 1/8!” more than one fifth grader shouted at the same time.

“No, that’s incorrect,” I casually, but cautiously counseled. Rewording what they had yelled in order to make plain the problem with their answer, I said, “You cannot make 11 AND 1/8 batches.” The emphasis on the word “and” did the trick.

“You can make eleven batches, and you’ll have 1/8 of a stick left over,” a student corrected.

“Perfect,” I affirmed. “Drawing pictures might seem silly, but look at how simple it is to see the answer. We didn’t do any denominator work past doubling up the number of sections in the last stick. I hardly did any math, beyond simply counting!

“When you are taking standardized tests, you get scrap paper. Use it. Draw pictures. Illustrate word problems. Take the time to label parts of your illustrations. Make sure that you understand what you are being asked. What is your goal? What are you supposed to find? It’s not just a number. It is the solution to a problem. In real life, it is a key that will unlock a problem. Be a problem-solver; Not a human-calculator,” I told them.

Photo by Elliot Fais on Pexels.com

In conclusion, my aim is to turn these advanced math performers into problem-solvers. With this goal in mind, I try to make lessons that force students to use what they have learned in their regular math class in a way that is not only compatible with what they would find in the “real world,” but forces them to understand how to use the skills. I often allow my students to use calculators because the problems I prepare for them require more knowing what to do with the numbers than practicing running through algorithms. AI can learn how to crunch numbers, but will it be able to successfully manage a kitchen full of amateur chefs laughing, telling stories, and making meaningful memories, all the while measuring butter for cookies after already cooking and eating a Thanksgiving dinner?

To combat the threat of AI, don’t try to make humans better than machines. That just makes them more like machines. I say, grow the human-ness of students. This is getting pretty deep, so I’m going to go eat a buttery cookie while I chew on these ideas for a future blog;)

Math Games: Dessert for Dinner?

What if you could produce a dessert packed with protein and healthy nutrients; I’m talking even more beneficial than a typical meal. Would you serve this delectable dish for dinner every day? My conclusion may surprise you.

Last week was Parent-Teacher-conference-week at my school. Students had half-days, and families either visited the building or used virtual conferencing tools to converse face to face with educators. This was the very first time that I bounced around from teacher to teacher, visiting the conferences of my gifted students’ parents. While there are many ideas that I could comment on, the one that stands out most was from the parent of one of my math enrichment students. 

The family has a third grader who is gifted, and that is why I was attending the conference. But, his little sister, who is in first grade, attends my math enrichment lessons, and it was something that she said that got me thinking. Her parents told me that they asked their daughter what she did in math enrichment class, and she told them, “We play games.” 

“Is that all?” I imagine them pressing, being the good communicative parents they are. Yup, is the first-grade answer:) 

This is a recent pic of 2nd grade learning to play Dominos.

I laughed when I heard their tale. I explained to the parents that I was teaching the first graders Dominos. After defending the fact that there is a lot of mental math and problem-solving, there was some light banter between parents and the regular ed teacher about only knowing the stacking and tumbling side of Dominos. 

Because their gifted third grader had already experienced lessons showing the critical thinking development of Dominos, it wasn’t necessary to get too defensive. They were “on board” with my use of games for strengthening math skills. But, the idea of my lessons being categorized definitively as nothing more than games gave me pause. Initially, I was perfectly okay with tricking students into learning through having fun. What teacher would turn down that strategy? “Can we have some more math enrichment, please!” the students whine. “Um… Yes!” every math teacher in the world would utter. 

Then I thought about the idea of turning everything into a game. Wouldn’t that be wonderful for the students? But, would it be healthy? Hmm… 

This is where the thought experiment at the top of this blog originated. I was musing over my math lessons being perceived as games, and I dreamed up the analogy of only eating dessert. Prepare to enter a rabbit hole of research. I’ll try to keep it palatable😉

History of Dessert

Asking “Why does dessert even exist?” feels a little like questioning the purpose of gold or jewels. Isn’t it obvious? It’s awesome! 

Believe it or not, dessert did not always exist, however. Similarly to gold and jewelry, it was discovered, and has evolved over time. The French are responsible for turning entremets into dessert (Gerson, 2019). Before there were sweets to end a meal, entremets were served as “interval” dishes, literally “between-foods” courses (Teppen, 2015). They were meant to cleanse the palate. They may be sweet, but not necessarily. 

Eventually, a final course of fruit, called le fruit, was formalized (Gerson, 2019). Only, before serving it, the table must be completely cleared. This cleaning of the table was called desservir, the French verb for “to clear.” More than tasting wonderful, the original final course of fruit developed into something lovely to gaze upon. Some desserts even consisted of “Elegant metal and glass structures holding whole apples or plums. Other times, meticulously crafted sugar figures became the center of dessert displays, and might not be eaten at all. Dessert specialists in the eighteenth century were supposed to understand architectural design and be capable of replicating it in sugar paste” (Gerson, 2019). 

These creators of dessert, as it came to be known around the time of the French Revolution, when the Bourgeois assimilated the term, were originally more like artists than chefs. Maryann Teppen (2015) writes of an entire battle scene, complete with tiny sugary soldiers with guns and canons, that told the story of Louis XV’s demise crafted out of sugar. It is hard to imagine your dinner table being cleared; plates, napkins, silverware, and foods being “dessert-ed” away; only to be replaced by an elaborate, sugary scene of violence that you feast your eyes upon but don’t touch!

Modern dessert serves a different purpose. BreezeMaxWeb (2022) suggests it psychologically signals the end of eating. Consuming a small, sweet treat at the conclusion of a meal might communicate to the body and brain that we are all done, and there is no need to nibble superfluous snacks. The End. 

A practice that I began a couple of years ago has helped me lose some weight and become more healthy; I will eat an apple at the end of every lunch. Many years ago I heard that apples help clean your teeth, and apparently there is some truth to that (Apples: Dental Hygiene Facts, 2017). Once I’ve eaten my apple, I cannot/will not eat anything else. I don’t want to undo my teeth cleansing. This has helped me de-snack my afternoons.

Let me reintroduce the concept of math games, here. Could a game be used to transition from one course of subject matter to another? Would playing a game cleanse the cognitive palate, and prepare students for something completely different? Of course! Would this be an appropriate way to signify we are done with the subject? I think so.

Delayed Gratification (Deferred Satisfaction)

How many parents use dessert as a reward for finishing a well-balanced meal? That treat is the ribbon at the end of a race. Some contests require more work and take longer, but when getting to the game of a lesson is the goal, students may trudge longer, work harder, and persist through all kinds of problems. Those students who finish first might learn patience through having to wait for their peers to catch up with them before the whole group can consume the dessert of a lesson together. 

Self control. Training. Conditioning. “If I let you eat this piece of cake, do you promise to gobble up all of your peas and carrots without complaining?” doesn’t just sound silly. I probably don’t have to tell you that this is an ineffective reward model;) 

These are this year’s 3rd graders (math enrichment), learning the game, Cribbage.

But, what if the dessert is carrot cake? What if the dessert is healthier than the dinner? Then what? “Eat all of your cake, or you won’t be given any peas…” Wait, what?!

Is there something to be said for learning to crunch through cardboard in order to earn cake? According to a longitudinal study spanning 40 years (Casey et al., 2011), learning and practicing self control early on in life can lead to better academic performance, less behavior problems, and even higher SAT scores. Casey and company (2011) describe in their paper, “Behavioral and neural correlates of delay of gratification 40 years later,” some ways kids can curb the pull of stimuli by learning cognitive control. There are mental strategies and tricks that people can use to provide buffers, dampeners, and walls to contain and maintain self sovereignty. Students may never learn or develop these important skills if they are never asked to wait for anything.

Through reading this research I wondered if teachers, themselves, are bypassing the delay of gratification when they jump right into games to teach. What educator looks forward to grumblings from their students? I propose that most  would prefer praise of pupils happy with pedagogical practices over the squabbling of scholars required to earn a fun activity. Are we educators partaking in dessert before dinner when we teach with games?     

Dessert Before Dinner

Before we beat ourselves up too much, let’s bring our metaphor along with us as we explore a couple of Jamarillo’s fun list of 11 Reasons to Eat Dessert First (2023). This may initially seem like a self-serving exercise, justification, or defensive maneuver, but hold on. Jamarillo raises the point that food can sometimes be a serious psychological hangup. “When we have disordered eating, we can often develop food or meal fixation.  Dessert is one of the most common food items restricted. This can lead to binge restrict cycles and disruption of hunger cues” (2023). 

Is it possible for students to develop “learning disorders” by experiencing “binge-playing” with learning games after enduring unnecessarily long restrictions? Just as Jamarillo (2023) suggests that dessert-first-eating can help overcome eating disorders through stimulating hunger, tapping into nostalgic memories, practicing navigation of bodily needs versus wants, and learning to respect cravings, beginning a lesson with a learning game can help students who struggle academically to open up to pedagogy.  

One thing more, and this might be a great way to end this blog, Jamarillo (2023) ends her short article with the fact that dessert is an ambiguous course. It can be a sweet, but doesn’t have to be. Fresh, raw fruit could serve as dessert. Pies, pastries, a tiny chocolate or candy, sweetened veggies, and yes, of course cake can all constitute desserts, whether eaten at the beginning of a meal, middle, or end. 

In conclusion, my first grade student may imagine all she does is play games during math enrichment time, but this learning dessert is rich with problem-solving proteins, mental math nutrition, and healthy higher-order thinking! With the short amount of time I have with my students, I have to make my challenges tasty. And, I’m okay with that;)

Sources

BreezeMaxWeb. (2022). Why Is Dessert Important After Eating Food?. Casa Romana Sweets. https://casaromanasweets.com/why-is-dessert-important-after-eating-food/#:~:text=When%20you%20eat%20dessert%20after%20your%20meal%2C%20it%20signals%20to,moving%20after%20you%20eat%20it.  

Casey, B. J., Somerville, L. H., Gotlib, I. H., Ayduk, O., Franklin, N. T., Askren, M. K., Jonides, J., Berman, M. G., Wilson, N. L., Teslovich, T., Glover, G., Zayas, V., Mischel, W., & Shoda, Y. (2011). Behavioral and neural correlates of delay of gratification 40 years later. Proceedings of the National Academy of Sciences, 108(36), 14998–15003. https://www.pnas.org/doi/full/10.1073/pnas.1108561108 

Cherry, K. (2023, November 5). The Meaning of Delayed Gratification: Deferred Satisfaction and Its Rewards. Very Well MInd. https://www.verywellmind.com/delayed-gratification-why-wait-for-what-you-want-2795429 

Apples: Dental Hygiene Facts. Summit Dental Health. (2017). https://summitdentalhealth.net/apples-dental-hygiene-facts/  

Gershon, Li. (2019, August 21). The Invention of Dessert. JSTOR Daily. https://daily.jstor.org/the-invention-of-dessert/  

Jaramillo, S. (2023). 11 Reasons to Eat Dessert First. Peace and Nutrition. https://peaceandnutrition.com/11-reasons-to-eat-dessert-first/  

Miller, K. (2019, December 30). What Is Delayed Gratification? 5 Examples & Definition. Positive Psychology. https://positivepsychology.com/delayed-gratification/  Tebben, M. (2015). Seeing and Tasting: The Evolution of Dessert in French Gastronomy. Gastronomica, 15(2), 10–25. https://doi.org/10.1525/gfc.2015.15.2.10

Multiple Enrichment Opportunities: Multiplication and Compatible Numbers with 3rd Graders

The idea underlying math enrichment is to deepen the understanding of math concepts that advanced students have already mastered. I began meeting with the top math students from each grade level (K-5) a few weeks ago, and I started off my introductions with this definition of enrichment. I didn’t want them to expect to go farther in their math skills, surpassing their peers. I also didn’t want them thinking that they were “above” their classmates who did not join me for this enrichment time. Rather than looking down from the mountain tops, we would dig in; We are in search of the riches (from en-rich-ment) that can only be found by looking beyond the ordinary teaching of math skills.

The challenge to myself is to find novel ways to show the use of math skills. I want the students to see that what they learn in the classroom is very necessary. Even if you never, ever have to use Pathagoream’s theorem, being able to use a formula correctly and understanding why is extremely valuable. 

An example of this is my lesson on multiplication for 3rd graders. Having completed an “Understanding Multiplication” lesson weeks earlier, and learning facts for multiplying zero through ten, I wanted to have students use these ideas creatively. I came up with a lesson that shows a way adults use multiplication all of the time without even realizing it!

There are four 3rd grade classes. Each one is very close to 25 students. How many students are in 3rd grade? Adults immediately know that there are about 100 kids in the 3rd grade. How? We instantly know that 4 X 25 = 100. Easy-peezy. But, there are a few things going on behind the scenes. We, grownups, are already rich in the knowledge of four 25s equaling 100, due to decades of dollars and quarters! Also, we know to use the compatible number 25 when numbers are close to it. Third graders have been taught how to round, but they don’t know that it is okay to completely change numbers into “easy to use integers” (compatible) for simplifying computations!

I told them that they could simply add all of the numbers together, first. That way they know what they are aiming for. But, they have to show the use of multiplication to complete the problem.

As always, I wasn’t going to just come out and tell them all of this. My math enrichment students had to dig for it, en-rich-ing themselves. I gave them this math problem. 

It has to do with them, which is fun. The numbers are accurate. I looked them up on the school’s database. These are the names of the actual third grade teachers. 

I read the problem to the enrichment students. Then, I asked them, “What is this problem about?” After the students identified the topic of third-grade population, we discussed what the goal was. You have to provide the total number of students, but there’s a catch; “You have to use multiplication to do it!”

When I walked the students through the Important Information; the data that will be used to solve the problem; I paused to point out some key elements. The students noticed the multiple 26s. I showed them that there was something else they all had in common; They were all in the twenties. There were multiple numbers with a two in the tens. 

Finally, it was time for the students to do their work. “Dig in!” I had put the word problem into a Google Jamboard, so I could make a copy for each student in the Google classroom that I’d shared with the enrichment students. They were able to write on the Jamboard, using their iPads. I walked around and witnessed the digging. It was awesome to see the variety of computations. When students told me that they were done, I showed them how to duplicate the Jamboard slide, erase their math, leaving the word problem, so that they had a new work space to solve the problem in a new way. 

After letting the students wrestle with the word problem for several minutes, I had students share their calculations. One student multiplied the totals of class sizes by 1 before adding them all together. “Does this meet the parameters of the problem?” I asked the class. Yes. “Is this useful, though?” No. The student had only done this after I told them to come up with multiple ways to solve the problem. I was glad they had, because it was an opportunity to point out making math work for you. “Multiplication is a way to simplify math, believe it or not,” I told them. “Can you multiply 20 times 4 in your head?” Yes; see? I reviewed with the group that multiplying anything times 1 is the identification principle. It simply tells you what you are working with; “One times Dominic, means you have one Dominic” 😉

I had students share their Jamboards on the classroom Googlel Jamboard, so we could witness the different ways to use multiplication. I was impressed by a few students breaking apart bigger numbers before multiplying. Only a couple of students recognized the closeness of the class sizes to the number 25. This presented a teachable moment, and I shared the vocabulary/math concept of compatible numbers. 

After this, our time was up. I mentioned that time, like money, presents some compatible numbers. “What is 4 times 15?” I asked the class. When no one answered immediately, I asked, “How many fifteens are in an hour?” They knew this to be four. “So… four 15s makes up one hour… ?” 

Sighs and “ah has” could be heard. “If you have a few numbers that are near fifteen, could you use fifteen as a compatible number for multiplication?” Hmmm… 

Average Salt Consumption: 5th Grade Math Enrichment

In the excitement of beginning a 5th grade math enrichment club I created a math problem that may have been a bit extreme. I wanted to use something from real life, make it challenging, and leave my students thinking. 

Photo by Castorly Stock on Pexels.com

The topic I settled on was sodium; specifically, our salt intake. What 5th grader can resist paying attention to a life and death lesson? They may have already heard about salt consumption severity, but if not, they will! This should make the lesson stick. (see “Explanation” of The Power of Contrast.) As it turned out, I was right. Not only did a few of the 5th graders understand the dangers of salt, but some knew that too much can negatively affect your blood pressure. 

In order to increase the cool-factor of the lesson, I explained the importance of salt in conducting electricity throughout your body. I did this by asking them which is more dangerous during a lightning storm, swimming in a chlorinated pool or a salt water pool. Salt is a much better conductor of electricity than regular, clean water. They were energized by this new information. (For a very easy to read article about salt’s necessary functions in our bodies, check out “Pass the Salt: Sodium’s Role in Nerve Signaling and Stress on Blood Vessels” by Abbey Bigler-Coyne. And, here is an awesome, short read about salt’s dangerous properties during lightning storms: “Ask the Physicists: Swimming in a Lightning Storm“)

I knew that the 5th graders had been working with decimals. I thought it would be fun to make a problem that had them wrestle with decimals in more than one way. We would average our salt intake. 

First, I did some research. According to the American Heart Association, humans would ideally consume 1,500 milligrams (or less) of salt per day. Written in decimal form, this translates to 1.15 g.

American foods are loaded with salt, and our favorites are the worst! For lack of time, I did not burden my math enrichment students with too much detail. They had no trouble understanding what foods are super salty. They mentioned French fries, hot dogs, and chicken fingers. Then, we discussed foods that didn’t seem salty, but definitely had some, like ice cream. 

This set me up for presenting my word problem: While the human body needs some salt (only around 500 mg), too much of it can be harmful. It is recommended to consume around ½ of a teaspoon or less per day. A half of a teaspoon of regular table salt measures about 1.15 grams. 

Some foods are notoriously more salty than others. In the interest of being healthy, one might try to consume less salt on days surrounding heavy intake periods. 

Look at the data to the right. How many days will this person need to consume only 1 gram of salt in order to bring their average down to 1.15 grams per day?

How It Works

Before going over the problems with my 5th grade math enrichment students, I taught what it means to find the average of a few numbers. I pretended that the students had taken a quiz, and I wrote some fake scores on the board. What was the average score? It isn’t necessarily the middle of the range (distance from smallest to greatest). I had written 10, 8, 5, 6, 8, 4, 0. (They insisted that someone get a zero; Rude! I suggested that the zero was probably due to the person failing to put their name on the quiz, and couldn’t get any credit;) 

There were two 8s. That might pull the average up. “You use an algorithm to find the average, and it can adjust,” I explained. I showed them how you add all of the numbers together, and then divide by the number of scores. “There’s more than one 8, so that should cause the average to weigh heavier on the higher end of scores. But, then the zero is going to drag the average down.” 

“It is like tug of war,” I explained. “The higher the scores, the more the rope gets pulled in that direction. If there are more low scores, the rope begins to go to that side.” 

We played with the numbers, changing them a few times. I showed how, when you raise a few grades, the average goes up. I had students make predictions. 

Next, I showed the 5th grade math enrichment team our word problem for the day. I read it to them, and then asked them our Ready Math questions that help us understand word problems:

  1. What is this problem about? A. Salt; Adjusting the average consumption.
  2. What are we asked to find? A. The number of days necessary to significantly decrease our average amount of salt consumption.
  3. What is the important information? A. The amounts of salt we consumed over the weekend, our goal, and the amount of salt we will allow ourselves to eat until we reach our average goal.
  4. And finally, what are you going to do? A. Continue figuring out the average of the three weekend amounts, combined with ones (1 gram per day) until you reach an average < 1.15 g.

They understood the story of the problem. We ate way too much salt over the weekend. Now, we feel the need to eat extra healthy to make up for it. 

I walked the class through one or two tries: “If you consume only one gram of salt during the day after the weekend, what happens to the average?” We added up the number of grams, and then divided by the four days in question. 9.61 ÷ 4 = 2.40, still too high.

I had placed the word problem in a Jamboard. When I pushed the lesson out to my 5th graders via their new 5th Grade Math Enrichment Google classroom, I made a copy for each. I let them wrestle with the numbers on their own for a few minutes. I showed them how you can “duplicate” a slide in Jamboard, so that all of the important numbers and word problem get carried over to another clean workspace. I wanted them to try the math a few times, showing me their work. 

I caught a few of them trying to average the three days of the weekend. I told them that this was unnecessary, because we already know that every single day of the weekend was way over our end goal of 1.15 g! “You can go ahead and practice averaging, but this won’t get you to our goal: Finding the day we don’t have to limit our salt intake to only 1 gram.” 

After a while, I wrote the weekend numbers on the dry erase board: 2.56, 3.08, and 2.97. Then I said, “What if you eat only one gram of salt for the next ten days?” I drew ten ones next to the first three numbers. “In order to find the average, you first add all of the numbers together.” I drew plus symbols between every number. “Next, you divide by the number of weights.” I walked them through dividing 18.61 by 13. “The average intake would be 1.43 grams per day. This is still too high, so we have to continue eating only one gram per day a little longer.”

We hadn’t found the answer by the end of our time together, but that was okay. This time of math enrichment was meant to provide teaching that they can bring back to class and use on their own during independent work time. I had hoped that some of the students would continue working on their salt word problem throughout the week, when they finish their other work. 

A few students seemed excited about finding the accurate number of days as they left the classroom. They told me their tries and expressed surprise at not finding the answer yet. I told them to keep going. It was out there!

I found out later that a few students expressed to their math teacher that the problem was a little too hard. This inspired me to include the next part of this blog; The explanation. 

I chose 1 gram to be the new amount that the person consumes each day because you could eliminate one of the steps from the algorithm for solving averages, if you used increments of ten days. More than erase the step, you do it mentally. We already did ten days in class. That wasn’t low enough. Next, try 20 days. If you remember that the three days from the weekend is 8.61 g, all you have to do is stick a two in front of it! Then put a two in the tens place of the number you are dividing by; 23 (twenty more days + the three weekend days). At this point, it would be best to use a calculator to figure out the long division. (I never said that you couldn’t. I modeled using long division, but once you leave the classroom… 😉 Just show your work!! Write down what you did. Document each try, the answer you got, what you did. Be a scientist about it. 

Once you find between what two tens your answer falls, you can begin narrowing your work further. 28.61 ÷ 23 = 1.24 (twenty days of 1 gram of salt per day); 38.61 ÷ 33 = 1.17 average grams of salt per day; close, but not there yet; 48.61 ÷ 43 = 1.13 We made it! …But, we only ate one gram of salt for more days than necessary. We overshot our goal. In order to figure out the exact day, we could go back one or two days at a time. Maybe try the middle; 35 days. 

One student messaged me within the 5th Grade Math Enrichment Google classroom, seeking clarification. She had taken notes on my example of ten days, and couldn’t remember why we added the ten to 8.61. I messaged her back, and a couple of days later, she had it! This student not only figured out the answer, but showed me all of her work. It is beautiful and impressive. 

In addition to this incredible success, however, I am pleased to share that some of the students were still mentioning the problem to me in the hall, days later. A student whom I see riding his bike when I monitor the crosswalk in the mornings queried if anyone had solved the problem, and we talked about possible solutions. I told him that it was more than 30 days. He couldn’t believe it. 

Congratulations to this amazing student! She did it. Great job!

Math With Chess

“How many more squares is White attacking than Black?”

This problem was awesome on a few fronts. Students had deciphered a Morse code message that shared a short sequence of chess moves written in algebraic notation. They played out those moves and discovered that one player had a huge advantage over the other. “How much of an advantage? Be specific. Can you put a numeric value to the advantage?” 

It all began with my preparing a lesson for chess club. I was going to teach club members about gambits. I researched the more common gambits and landed on the Smith Morra Gambit. I found a succinct video on Youtube that explained the gambit. While watching the video, I wrote down the algebraic notation. 

But, I wouldn’t just give them the chess code to learn the gambit; I decided to have my gifted students decode the code! My fifth grade gifted students were the first ones to see the code. They had only dabbled with decoding Morse messages. 

I had used Morse Code Translator to change the chess play sequence into dots and dashes. Rather than writing the number of the move; This was going to be confusing enough as it was; I decided to change the colors of the moves. White’s moves were turned to white dashes and dots. I made the background of the text box green, so that you could easily see the white and black codes. I put an image of my code, along with the Morse Code alphabet and accompanying numbers onto a Google Jamboard. The fifth grade gifted students were on it the moment they walked through the door. 

The two things that I shared with the fifth graders was that the slanted line (/) separates the words; In this case it broke up the moves, but I did not explain that. I told them nothing about the actual message. The second thing that I pointed out was where each letter or number’s code ended. The translator that I use makes it much easier and faster to produce Morse Code, but sometimes it is difficult to locate the space between each letter/number. After pointing out these two key factors, I stepped back and watched the struggle. 

Right away I heard a couple students divvy up the White and Black “words.” I was glad to hear the idea of collaboration. I wondered how long it would take for someone to understand that these were not actually words. The very first coded move was e4, the most popular opening move in all of chess. I heard a few people verbalize bafflement, but several recognized the move, “It’s chess!” someone shouted. 

I didn’t help them with any of it. At least one student knew enough to be able to read most of the algebraic notation and make sense of the moves. Of course I had a chess board and pieces handy, and we set up a game. I let the students figure out the sequence of play. When they came to the gambit on the second White move, I stopped them to explain what a gambit was. This was good practice for my chess club lesson that afternoon. A couple kids would get a double lesson, but that was okay. They could be my co-teachers! 

“The word gambit is closely related to gamble. It means taking a risk. A chess gambit happens when one player offers up a peace as a sacrifice in order to draw an opponent into a trap or sequence of moves that would benefit the aggressor (the one offering the gambit). Do you capture the sacrifice or risk the piece taking your own?” 

I had the fifth graders play through the short sequence until Black’s pawn was captured. Black had accepted the gambit, capturing the initial White pawn placed on d4. White offered up another pawn on c3. When Black captured that, White might feel a little on edge, because now there is a Black piece threatening the second rank of the White team! It is so close to attacking the Queen!! 

Before any more damage can be done, White captures with the Queen-side Knight, Nxc3. White has lost two pawns, while Black is only down one. If you were to only count points, it would appear that Black has the advantage, being up a point. A mere glance at the board should show even a novice player that White is in a much better position!

I explained to the fifth grade gifted students that the best thing to do at the beginning of a game of chess is to control the middle of the board. With that criteria, everyone can easily see the trap that Black has fallen into. There is a White pawn left sitting on the initial e4 square. And, now a Knight is “developed,” backing up the e4 pawn and attacking four more squares (b5 and d5 as well as a4 and e2).

The fifth grade lesson stopped there, but my fourth grade gifted students got a treat. It only took seconds for them to figure out that the Morse Code message was algebraic notation for a chess game. When I heard some groans, I told them, “The first to solve the riddle can play me in a game of chess.” Now, the heat was on. I set the board back up in the middle of a table while my students grappled over letters and numbers seemingly unrelated to one another. 

We worked through the Smith Morra Gambit sequence the same way I had with fifth graders. I had the fourth graders figure out the algebraic messaging. They figured out that the Xs meant a piece had been captured. I had to explain that the “d” in dxc3 meant that the capturing pawn had come from the d file. After explaining gambits and discussing the advantages and disadvantages of the board we were left with, I played a blitz round of chess against a pair of students.

Third grade was next, and these students are not only classy, but they are some of the hardest workers I’ve witnessed. Their grit knows no end. I presented them with the same problem. They labored through decoding my Morse Code message. We played the sequence out. I taught them what a gambit was, and we discovered the significant advantage that White was left with. But… Then I was hit with a question that I liked so much that I recorded it on video so that I would remember it: “We know that White has the advantage, but how much of an advantage? Can we put a number to it? How many more squares is White attacking than Black?” 

Not all of my third graders know how to play chess. I taught the team how each piece attacks. “How many squares is the King attacking?” I asked. I showed them how it moves. The answer was two squares. “How many squares are the Bishops attacking?” We looked at their lines of attack. I showed them the squares that the Queen attacked, including the Black pawn on d7. We went over how a pawn attacks diagonally and the way a  Knight moves. Then I set them loose.

A few floundered, so I guided them to make a T chart. “Let’s do one color at a time,” I suggested. “Also, how about we focus on only one piece?” We carefully counted all of the squares that the Black pawns were attacking (12). Then we counted up the Knights’ attacks (4).

Next we moved on to White. There was an empty square next to the White Rook, so that counted as an attacked square. We continued counting until we covered every piece. I missed a couple of the the Knight’s attacks, but Gray got my back. She caught my mistake, and we corrected the calculation.

In the end, we discovered that White was attacking 43 squares to Black’s 16, way more than twice as many! So, was the gambit worth it? I’d say so. And, what could Black do differently to limit the massive advantage? Don’t fall for it. Don’t take the gambit. Push forward or ignore, but definitely think ahead.