Developing Real-World Math Problems: Adding & Subtracting Mixed Numbers

During an interview for a podcast with Curriculum Associates the other day I was asked how I use real world scenarios to enrich math lessons. I had explained to the interviewer that teaching is a second career for me. My experience of entrepreneurship as a residential custom painting contractor helps me introduce loads of business expertise in my math lessons. 

Blog about using tile cutting in a math lesson
Blog about using wallpaper hanging in a math lesson

The interviewer was looking to provide practical solutions for teachers to use. I took two seconds to imagine I was sitting in front of my computer (as I am right now;) and tried to remember the steps of making my lessons. 

The first thing I do is find the lesson in the i-Ready toolbox, and look at the “Extend Learning” assignment. I don’t usually use the i-Ready assignment verbatim, just in case the regular education teacher wants to assign it. I use it as a guide for my enrichment lesson. 

i-Ready provides paper lessons that can be assigned virtually or printed out.

For instance, this week my fourth graders were learning about adding and subtracting mixed numbers (Lesson 21). The extended lesson shares a story about a couple of kids filling a fish tank. Some mixed numbers are used, and kids are asked to do calculations that would require them to add and subtract the mixed numbers. 

Here’s a GIF I made showing our classroom 75 gallon fish tank. I made the stand that it is sitting on out of 4 X 4s.

I actually have a 75 gallon fish tank in my classroom, so this story could very well be perfect. However, I just wasn’t feeling the mixed number connection. There is no way that three friends would have three different buckets that all hold different mixed numbers of water with a fraction containing the same denominator. It felt too implausible. 

Regular Ed teachers could still use this paper assignment about students using mixed numbers to fill a fish tank.

I sat at my computer and thought, Where do I encounter mixed numbers? In addition to having run a successful business, I’m also a “Do it yourself-er.” I enjoy building things. Making things with my own hands and tools is satisfying to me. I made the stand that my fish tank sits on. I finished my own basement, complete with bathroom and laundry room. In short, I have come across plenty of mixed numbers! Developing an enrichment math lesson that uses mixed numbers will require me to make the work of adding and subtracting the mixed numbers both doable and easy enough for the fourth graders to understand. That is my challenge.

When I say that I like to use my hands to build things, I don’t mean paper airplanes. Check out this blog about my giant wooden sunken pirate ship classroom decoration.

The morning that I came up with “Fix a Bench” my first thought was to have my students figure out how many boards would fit on a small deck surface. Each board could be a mixed number in width. This would be similar to the fish tank assignment from i-Ready. Kids would just add them up to fill the space.

As I began researching and looking for pictures online to jazz up my presentation, I remembered that lumber is full of mixed numbers. The most common building material, the two by four, is NOT really two inches by four inches. I learned this ages ago when I expected several adjacent two by fours to equal a nice even round number. It was some wacky measurement, and I took a closer look at the dimension of the studs (two by fours) I had purchased. I was incredulous, thinking I’d been ripped off! 

Thinking this might be a fun fact to share with my students, I decided to have them explore having to use various sized pieces of lumber to make something. The fourth graders love mysteries, and I would wait until the very end to explain why two by fours are called that when they actually aren’t those dimensions. 

My lesson was originally “Build a Bench.” When I began planning what my students would actually do, however, I figured out that it would be easier to teach and explain if I had them only choose lumber to place onto an already existing frame of a bench. Thus “Fix a Bench” was born. 

The next part of developing a good real-world lesson is to create a “Sell.” You must come up with a pitch to draw the students in. “Today we’re going to fix a bench” isn’t good enough. Instead, I told my students that “It’s your parents’ anniversary (or birthday for single-parent families), and you want to give them something, but you have no idea  what! They have a special bench that they like to sit on, but the wood is rotting. You get the idea that you will fix this bench for them as a gift. Because you don’t have enough money to buy the wood to do the work, your parents agree to get it for you. Your labor and thoughtfulness is the present. In exchange for your parents footing the bill, you have to tell them exactly how much the lumber will cost.”

This little story makes sense to the students. Even if they don’t have a bench in their backyards or don’t have a backyard at all, they can imagine doing this kind of thing. Also, it gives them some good ideas of how to come up with presents for their parents that won’t cost them anything more than creativity and thoughtfulness. 

“How much does the wood cost?” the students instantly want to know. 

“Before I tell you the costs, I am going to need a helper… This person has to have very good penmanship. I will know that they can write very neatly by how well they listen to the explanation of the project…” I share this with a very stern look in my eye, as I scan the room for anyone not paying close enough attention. Every student straightens their body and widens their eyes. I proceed to share the dimensions of the bench frame.

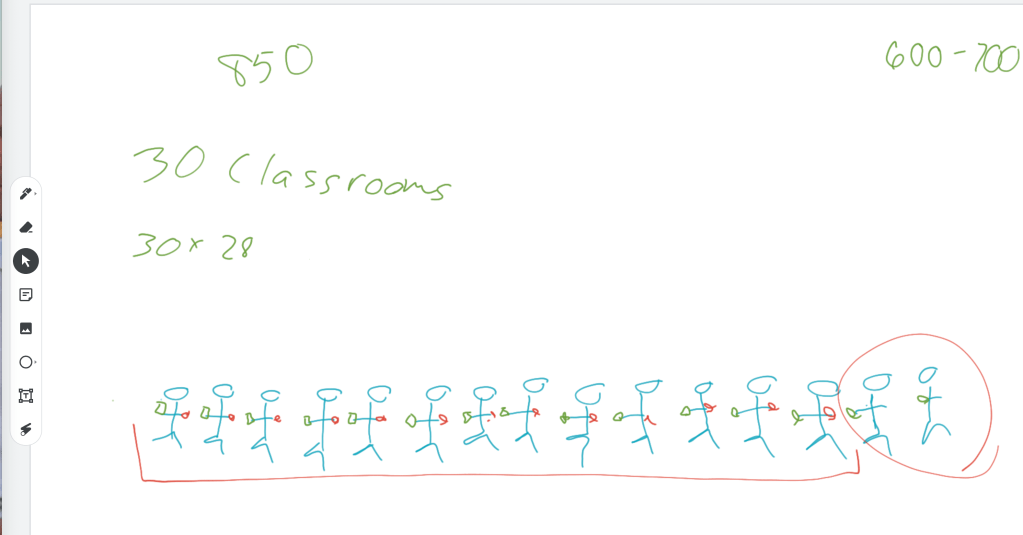
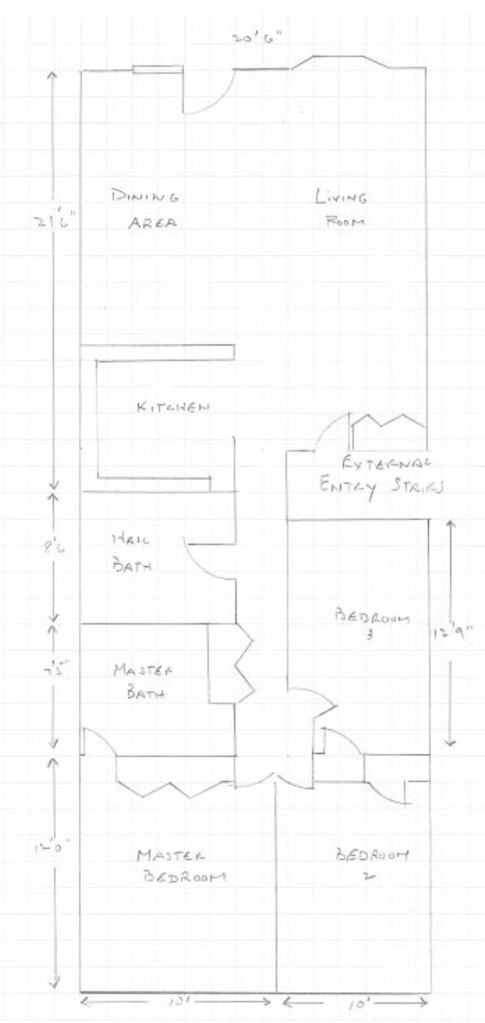
I got the size of the bench by measuring one of the chairs in my room. The back was approximately 16 inches tall, and the seat was 14 inches deep. Instead of supplying these simple numbers, I turned them into mixed numbers. Sixteen inches turned into 1 ⅓ feet, and 14 inches transformed into 1 ⅙ feet. In order to narrow the focus of calculations, I made the bench exactly eight feet wide. This way, there wouldn’t be any trimming of the ends of the boards. Just choose eight foot long pieces. 

Now, it was time to show the students the materials available to them. I had found a list of lumber online that showed the names of the wood with the actual dimensions next to them. With this image on the screen in front of the class, I showed students how a two by four is actually 1 ½ inches by 3 ½ inches. A two by six, another common board measurement, is really 1 ½ inches by 5 ½ inches. And, a two by eight board is 1 ½” by 7 ¼”! 

The class needed a little guidance to get started with this lesson. I guided them through drawing a diagram of the important parts of their bench. We labeled the back, the seat, “And don’t forget about the single board that goes on top!” I told them. I had them figure out how many inches the mixed numbers would translate to. “Now, we have to fill these spaces (16 and 14 inches, respectively) with lumber,” I told them. “It would be easy if two by fours were actually two inches by four inches, but they aren’t! See if you can figure out how to make sixteen inches of surface using these mixed numbers.” I circled the widths of the “two bys” from the image. I had told them that we would only use those, because they need to be thick enough to hold a human’s weight. 

Using only 3 ½ (the width of a two by four) won’t work for the back of the bench. My students figured out that four of these boards will get you to exactly fourteen inches of wooden surface. That leaves you with a two inch gap, and “We don’t want any spaces. Neither can we saw any boards to resize them. There aren’t any boards that are exactly two inches wide. Can you take away one of the two by fours, and find a different size board that fits nicely?” 

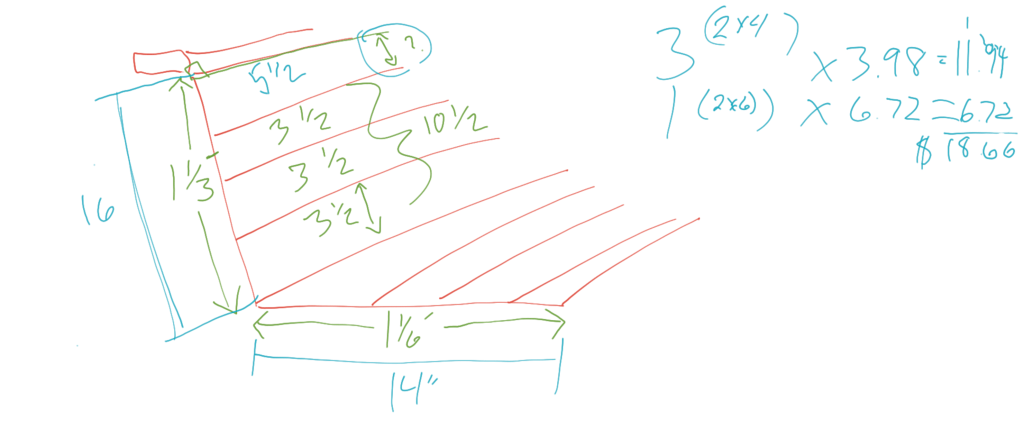
When my students take 3 ½ away from fourteen, they have 10 ½”. “What is the size of the space, now?” I ask this while pointing to a gap that I’ve illustrated on my drawing of the bench we are fixing. They figure out that the empty space is exactly 5 ½ inches wide. “Are there any 5 ½” wide boards that we can purchase?” Yes. The 2 by 6 is that width. 

Are we done? Definitely not! “You were all such hard workers and very good listeners that it is very difficult to decide who could be my writer,” I tell my class of math enrichment fourth graders. 

One of the students actually volunteered another, saying, “Nahum has really good hand-writing. You should have him write on the board.” 

“Are you nominating your friend?” I inquire. He admits it, and several students second the nomination, suggesting that Nahum really does have good handwriting. “Well, okay, then. Come on up here,” I extend the invitation and commend Nahum’s friend for being classy.

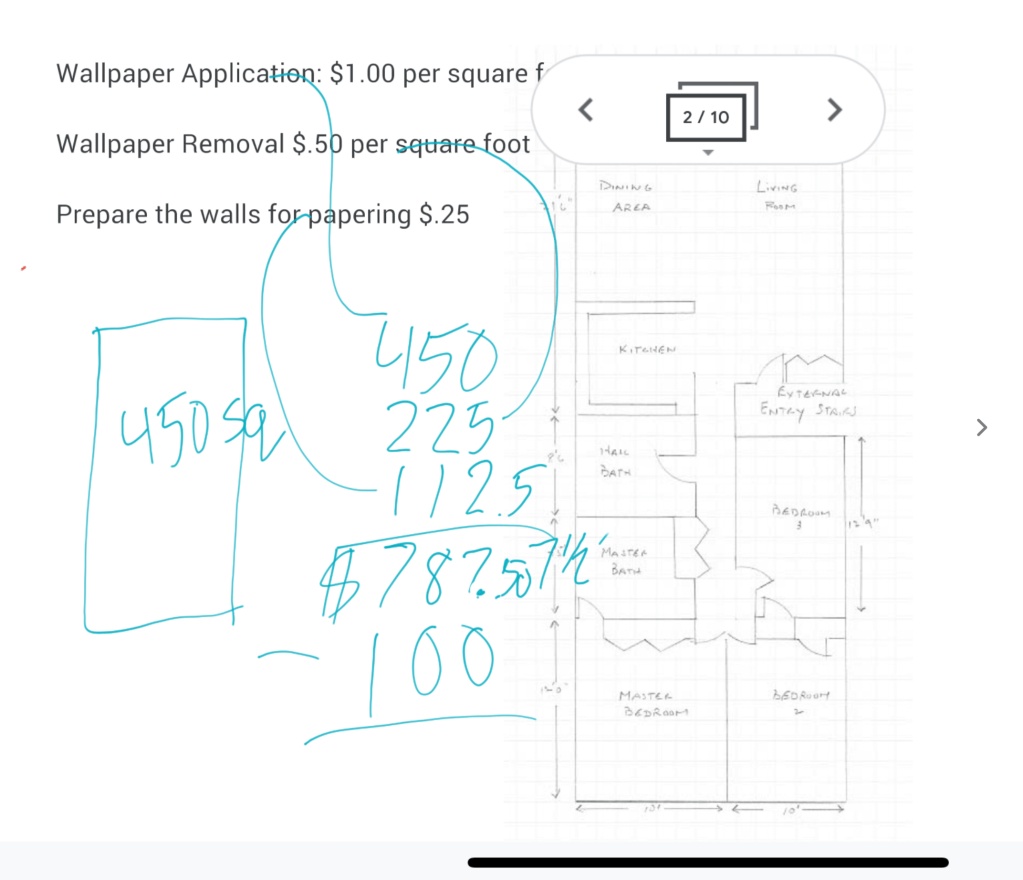
As Nahum prepares to write on the board, I open my laptop. I have pricing from a lumber yard ready to go. We now write down the amount of money each board will cost us. I have Nahum give the writing tool to other kids after he writes a couple of prices, so that more students get a chance to write on the board. We only supply the prices of the two-bys, because those are the only ones we are using. 

Students proceed to figure out the cost of 3 two by fours and 1 two by six. When they think that they are done with the project, I point out that we still have to figure out the seat of the bench. They happily begin problem-solving that challenge independently. It took a surprising amount of time for them to figure out that we had already answered the question of what boards could be used. The 4 two by fours that we had added up earlier had totalled exactly fourteen inches, which is the size of the seat! 

When they began adding up four prices of two by fours, I pointed out that we already knew how much three of them cost. “Why not just add the cost of one more to the first number?” I suggest. Grateful for the idea, they do this. 

Preempting the “I’m dones!” that were about to fill the room, I reminded them, “Don’t forget about that top board… The one that goes on the top of the back of the bench.” Happy groans and more pencil scratching ensued. 

Just when my students thought that they were finally done, and Mr. Weimann couldn’t come up with any more surprises, I told them, “It would be very classy if you figured out how much your parents would have to pay in sales tax.” Epic groaning accompanied smiles and students beginning to hunch over their iPads. I told them to use calculators and that our state sales tax was six percent. This was the icing on the cake. 

After a few seconds, I modeled for them, asking Siri, “What is six percent of thirty-eight dollars and fifty-six cents?” When she told me, I wrote it on the board for them. 

Because I had created Google Jamboards with all of the information preloaded on them, I was able to see each individual students’ work. I had waited until Nahum and partners had neatly written the prices into the slide with lumber details before I pushed the Jamboard out in a Google classroom assignment. I had the software “Make a copy for each student.” Students knew that, although they were allowed to work with partners and I helped them solve several parts of the problem on the board, they had to add their own version of the details, showing their work

Before students left my room I explained why two by fours are actually mixed numbers. The lumber is cut at exactly two inches by four inches, but when it dries, it shrinks. Of course the students wanted to know why lumberyards don’t correct for this or call the wood by another name. The young minds cried foul and felt tricked! I told them that it has been this way for a long time, it is easier to say “two by four” than “one and a half by three and a half,” and the price of the wood that you feel like you are being cheated out of goes into having to store it while it dries, before selling it. It isn’t like the mill cuts a two inch by four inch pied of wood for you to bring home, you build with it, and it shrinks on your home. That would be worse. In the same way that creating this lesson required several steps, when one wants to make and use a two by four, you measure the wood, cut the lumber, let it dry, measure it again, and then you can work with it.

Comparing Fractions Through Arch… itecture

Humans love to construct (Lorek, 2018). Is it in our instinct? Sarah Lorek (2018) contrasts the idea that beavers building a dam would be considered “natural” versus humans constructing a dam being “man-made.” The structures look different, and have slightly different purposes, but the reason for construction may not be as disparate as assumed. 

[I searched the web for articles that speak to the (my) hypothesis that constructing things might be a human natural instinct and came up short. This would most likely be a very difficult thing to prove, but I’d love to read about it. If anyone knows of any literature or can point me in the direction of a good source, please share.] 

From my own personal experience, I can say that I have witnessed students come to life when building blocks are made available, and some of my favorite activities involve construction. I have fond memories of sitting in the middle of a mess of Legos, Lincoln Logs, and Robotix when I was a kid. I spent hours building spaceships, cities, and robots. Now, I remodel my house (recent bathroom project), labor on landscaping, and generally enjoy working with my hands (famously failed pirate ship project).

I’ve written about the unique and exciting experience of putting building materials in front of my students. From Building Bridges, using Blocks to teach measurement, Adding Blocks, Purchasing Blocks to use in business plans, constructing Bridges as Object Lessons to teach SEL, and creative Playtime, my students are no strangers to building materials and hands-on lessons. Even during this past lesson, I heard students professing this to be the best Math Enrichment lesson, yet! 

Purpose

Students have been introduced to fractions in their regular math classes. I was planning to enrich a lesson about comparing fractions. Our math curriculum had a nice worksheet that would have students create quilts with limited colored squares, and then compare the fraction of each color. Students can still do that lesson, but independently in the classroom. I created a lesson that was hands-on and interactive.

Students would use colorful connecting blocks to construct an arch. I had a picture of the arch in Washington Square, NYC on the board when they entered the room. We discussed the idea of arches for a few seconds before I shared the parameters of the project. 

Arches are symbolic, letting in light and allowing people to walk through walls. They are old; developed during the second century B.C. They are also timeless, in that they are still used today. They have even been known to hold magical properties! Vampires must receive permission or an invitation before entering someone’s home (through an arch), and the arch makes an appearance in Harry Potter as a passageway between this life and the beyond.

A memory that popped into my head that will definitely date me is that of the movie “Ernest Goes to Camp” (1987). The image on the cover of the movie shows the arch that Ernest is working on at the very beginning of the movie, surrounded by several scenes from the flick.

Parameters

As per a recent lesson that I learned about setting tight parameters, I constructed very strict limits on student creations. Students were allowed exactly 24 cubes. I chose this number because we have been learning and playing Math 24 a lot recently, and because the number 24 is divisible by many numbers. The lesson could include reducing fractions, making common denominators, and more through starting with 24 for a denominator.

The blocks could only be red, green, blue, and/or yellow. At least three different colors were to be used. This ensured that there would be some comparisons between fractions. 

Students could work independently or with a partner, but no groups larger than two. Each student, whether working with a partner or alone, would be responsible for putting information about their project into a Google classroom assignment. 

Activity

Once the assignment was explained, I set them loose. They were busy bees, buzzing around the blocks, loving the building. Creativity bubbled in the classroom. There was a purposefully leaning arch, decorative arches, symmetrical aches, one was made as short as possible while still fulfilling the definition of “arch,” and one even mimicked the pointed style of the Gothic Arch. So impressive! 

I stopped the students when some of the first arches were being completed, so that I could instruct them on what to do next. I had a couple of girls hold up their arch for an example. We took a photo of it, which is what I wanted everyone to do. This way, I could assess the accuracy of the numbers. It demonstrated to students that they must provide evidence.

I model taking a photo of the photo I just took after teaching what to do.

Next, we counted the number of different colored blocks. The girls had made their arch symmetrical and used the same number of colors for each of the three colors. (This is something I fixed the next time I taught the lesson, that afternoon; “None of the colors can be the same number.”) 

I showed the students how to write the fractions next to the color of blocks that I had provided for them in the software that they were manipulating. Then, we wrote an equal sign between the two fractions. The way I got the girls to include “greater than” and “less than” in their project was by combining colors. “The fraction of cool color blocks was greater than the fraction of warm color blocks.” 

Time was allotted for producing fractions and making comparisons on iPads. In order to do even more comparing of fractions, I then had students take pictures of a neighboring team’s arch. They then imported that photo into their Google Jamboard project so that both their arch and their neighbor’s arch were side by side on a slide. Now, they got to compare the fraction of red blocks from their arch with the fraction of the other arch that was constructed with red blocks. This exercise involved talking about the math, sharing out, and self assessing. 

In the end, students enjoyed not only comparing fractions, but constructing them, building knowledge, and cementing learning into a fun and memorable experience. 

Sources

Azzarito, A. (2021, August 19). From Architectural to Artistic, Arches Are Trending. SemiStories. https://semistories.semihandmade.com/design-history-arches/

Lorek, S. (2018). Ancient Architecture and the Human Need to Construct. Trimble Construction. https://constructible.trimble.com/construction-industry/ancient-architecture-and-the-human-need-to-construct  

Sinclair, L. (2014, December 19). The History of Architecture in Eleven Arches. The Architectural Review. https://www.architectural-review.com/essays/the-history-of-architecture-in-eleven-arches

The Top 10 Construction Toys of All Time. Michigan Construction. (2017, December). https://blog.michiganconstruction.com/the-top-10-construction-toys-of-all-time

Pedagogical Aikido

“Where did the 850 cans come from?” I was in the middle of sharing the iReady enrichment lesson (14) with my fourth graders when one of them asked me this question.

Have you ever had a student ask a question in order to postpone learning? If you’re a teacher, then that’s a silly question. Of course! 

This is one of the few things that I remember from my elementary and middle school days. It was a thrilling challenge to try to come up with just the right topic or question that could throw the teacher off track. 

We would hope and pray for a story. Then, we would artfully flatter and ask questions that would lead our pedagogue down the rabbit hole of memories, further and further… away from the lesson at hand. 

Fast forward forty years. Today’s students still play the same tricks on their teachers! This past week I was engaging some fourth graders in math enrichment, when one of them tried steering me off task. Little did they know, that I practice Pedagogical Aikido. 

Redirecting Energy

Aikido is a form of martial arts that is known for using an opponent’s energy (ki) against them. Masters of this study practice redirection. 

Although I have not formally studied Aikido, I love its principles and attempt to use the philosophy of redirecting thought and energy within the walls of my classroom as much as possible. 

For example, the other day when my student asked about the origin of the 850 cans in our math problem, I allowed the student to think that he had derailed the lesson. I told him that this was an excellent question. “850 cans is a lot of cans. Where would a school get that many cans for a fundraiser?”

The martial art Aikido uses a triangle to teach the redirection of energy. There are three components that work together to use an opponent’s attack against them, saving your energy and neutralizing the situation. It all starts with Balance, known as tachi waza (Aloia, 2020).

“How many students does our school have?” I asked the class. 

I could have squashed the student’s inquiry, telling him something like, “I don’t know where the number of cans came from. It’s hypothetical. Let’s just move on!” Or, “It came from Curriculum Associates, the authors of our math program. Don’t ask silly questions.”

If I had done that, I would have disrespected the student. A dismissive teacher or one who blocks the question head on is too hard, too strong; the lesson too one-sided. By allowing for the question in the first place, and then entertaining it, I had my center of gravity low to the ground. My metaphorical feet were spread wide apart and knees bent. The question didn’t topple my lesson. I was balanced.

In answering my question, the students were surprisingly accurate. Our school has around 700 students. “How many cans would we have if each student brought in one can?” I prompted. That was easy. “But, not every student will bring in a can… And, some will bring in more than one.” The easy back and forth of these simple concepts established a flexible, down to earth ease of thinking. It also revealed the problem. We don’t know where the 850 cans came from.

Next, it was time to Break Balance. This is the second part of the redirecting-energy triangle. “The opposite of balance is imbalance, or kuzushi. To break an opponent’s balance, one must first redirect their energy to one’s own advantage” (Aloia, 2020)

I shouldn’t be surprised, but I was very impressed, nonetheless, at how quickly my students figured out how many classrooms our school had. It was the advanced fourth grade math students receiving enrichment, after all!

I had begun the imbalance kuzushi by getting the class to come up with the total number of classes in the building. After figuring out that our school has five classrooms per grade and our school teaches six grades, if you include kindergarten, we discovered that there are 30 classes represented.

“Let’s say that our school collected 850 cans. How many cans would each class bring in?” The students had no clue where to start.

Antonio Aloia (2020) explains that kuzushi has two arms. The physical off-balancing of an attacker, parrying the opponent’s strike and redirecting the momentum of the assault, coupled with a strike of their own is what one normally thinks of when imagining Aikido. Um, of course there isn’t any literal physical contact with students, let alone “attacks,” but presenting this new problem of dividing up the number of cans by the number of classrooms was a cogitational assault of sorts.

The other arm of kuzushi is a psychological off-balancing. This is where a martial artist would “Distract a would-be opponent by bringing their attention to something else, be it an object on a building or something farther away and behind the opponent” (Aloia, 2020). Pedagogically, this happened when I changed the student’s original question from “where” to “how”: “Where did the cans come from?” turned into “How could a school come up with so many cans?”

While the martial art of Judo involves throws, Aikido keeps your opponent tight and controlled. Perhaps counter-intuitively, it is concerned with the well-being of the attacker. So, rather than toss my students aside to flounder with the problem of dividing 850 by 30 on their own, I guided them through the process of figuring out the answer.

I asked them how many cans there would be if every class brought in 10 each; 300. “Okay, maybe that was the first week of the fundraiser. If each class brought in another ten cans during the second week, how many cans would the school have collected?” We were up to 600 cans. They were starting to catch on. 

One of the students used Google to divide 850 by 30. Rather than scold him, I asked him if it were possible for any of the classrooms to bring in .333333 of cans. This was a silly question. “What happens with the remainder from the division answer?” I asked. They didn’t know. “For our purposes, we will assume that the students from every classroom brought in 28 cans. The teachers brought in the rest.” My students were okay with this explanation. 

The third side of Aikido’s redirecting energy triangle permeates everything. It is ki or energy. Don’t think of it as power or force, though. Ki is more like momentum.

“How big are our classrooms? How many students are there in a classroom?” I got several answers on this. We decided to use the number 20. “Let’s say that a quarter of the students don’t bring in any cans. If the rest are responsible for bringing in 28 cans, how many brought in two and how many brought in one?” My students just looked at me. I told them to try and figure it out on their own, and then I’d show them. 

One student crushed it, and I had her show the class what she did. Then I modeled drawing a picture to solve the problem. 

After all of this, I told my students, “Now that we have collected all of these cans, we need to put them in something to bring them to the food pantry that we are donating them to.”

“If Dylan went out and bought a bunch of boxes… Thank you Dylan! (Dylan is all smiles at this point; He may or may not have been the person to ask the question that started all of this;) And, if Dylan’s boxes are all the same size, holding six cans each, how many boxes would Dylan have to get?” I let them wrestle with that a little while. 

When I was prepared to let them demonstrate their math on the board, I turned to the slide that had the original question on it. They reread the word problem as I decided on who would come forward to share their work first. A few students groaned and some others called out. “That’s the problem we just did!” 

“Yeah?” I feigned ignorance. 

I used someone else’s name when I told the story about getting bigger boxes; Ones that held 8, instead of 6 cans. “How many of those boxes were purchased?” 

As it turns out, we never got to fully explore the last question, but a couple of students tried solving it in their heads. I had completely Aikido-ed them! Lol.

Redirecting energy can be an even more effective motivator than a cool lesson. Take their energy, spin it around, and use it against them. Students will feel like they’re in charge of their own learning, and in a way, they are!

Source

Aloia, A. (2020, June 19). Reflecting on Jujitsu Pioneer George Kirby’s Advanced Techniques for Redirecting an Opponent’s Energy. Martial Arts of Yesterday, Today and Tomorrow. https://maytt.home.blog/2020/06/19/reflection-on-jujitsu-pioneer-george-kirbys-advanced-techniques-for-redirecting-an-opponents-energy/comment-page-1/?unapproved=2695&moderation-hash=f6966939a4ca212a2123a94cabda8d13#respond

The One-Room Schoolhouse Game

The other day my elementary school had an assembly. When it was over, a fourth grade class was left with no teacher. She had attended a meeting that was running over. Since I didn’t have a class at the moment, I decided to bring her students upstairs for her. As we waited in the fourth grade classroom for the teacher to return, I wondered what I would do to maintain a semblance of sanity. I decided on a game centered on behavior: The One-Room Schoolhouse Game.

When the teacher, accompanied by an instructional assistant (IA), entered the room, they couldn’t believe their eyes. Every student was sitting up ramrod-straight. Every single eye was trained on me. The IA verbally queried, “What is happening in here?” She was incredulous. I was in my element.

Educators are show(people). We are either putting on a performance to attract the attention of our students. Or, we are ringmasters, making sure the mayhem stays within the bounds of 42 foot diameters (the official size of a circus circle).

This is an image of the Claussville One-Room Schoolhouse, the same that my class visited on many field trips.

There are many ways to perform, but methods for maintaining order is more limited. Many years ago I came up with a unique way to do both at the same time. 

When the IA, who had seen the game in action, entered the faculty room at lunchtime, she practically burst with enthusiasm, announcing to the other teachers what she’d seen. Some of the staff members wanted in on this game of good behavior that students seem to enjoy. I explained the rules to them. Since then, I’ve had a couple of teachers ask me to share with their classes how the game works. I’m more than happy to oblige.

Then, I searched my blogs to see if I’d written about The One-Room Schoolhouse Game. Unbelievably, I hadn’t! So, here goes.

It began many years ago. I brought my 3rd grade class of “Polite Pirates” (what I called my group of students) on a field trip that visited several historical sites around our area, all in the same day. It was a fast-paced adventure of a field trip, running from one stop to another, practically assaulted with information. 

I made this video from photos and video of my 2016-17 class visiting Claussville.

We began the day at Trout Hall, the original house of the Allens, the family that founded Allentown, Pennsylvania. The building is staged to look like it had during the Revolutionary War era. A tour guide led us around the house and explained many interesting facts. 

Students get to ring the Liberty Bell replica.
Students explore the replica of a Conestoga wagon.

From there, we traveled only a few blocks away, where the Liberty Bell had been housed during a portion of the Revolutionary War, hiding it from the British. The Liberty Bell Museum has a life-size replica of the original bell, a slightly smaller than lifesize model of the wagon that would have carted the famous bell, along with several others from Philadelphia to our town. They have a nice mural and story display that they show. They also provide a favorite feature of every field trip; a gift shop! This is where I acquired my famous “One-Room Schoolhouse” bell. It is a mini replica of the Liberty Bell.  

This is my 2021-22 class in front of the Claussville One-Room Schoolhouse.

The final stop of the day was  an old school building that was preserved to look the way it had when it was used as a one-room schoolhouse as late as 1956. The Claussville Schoolhouse is where I learned the practices that what would turn into the rules of my One-Room Schoolhouse Game. 

A tour guide walked us through what it would be like to go to school one hundred years ago. Every grade, from first through eighth was taught in that one room! Because of this, the school master had to be very strict. 

I explain all of this nowadays when I introduce The One-Room Schoolhouse Game. Believe it or not, me acting like a big meanie is one of the more fun aspects of the game! Students love tempting me to pretend to yell at them. Suffice to say, this is far from my typical conduct. 

The Game

Now you know where the idea for the game originated, let me explain how it’s played. I introduce the game on the very first day of school. It contrasts the comfortable social/emotional learning (SEL) environment that I foster and points out how nice I actually am. 

Right off the bat, I talk about what school was like a hundred years ago. Because there weren’t any buses, schools only serviced local communities. Every kid walked to school. The building housed every grade, from first through 8th! A teacher was responsible for managing lessons for eight grades, all at the same time. And, there was only one teacher. They could not afford to have any disorder or misbehavior, so the teacher was very strict. 

“There were many rules for doing things. First of all, the students had to sit up straight.” As I say this, I morph into a very serious, demanding persona. Every student whom I have ever shared this game with has always straightened his/her posture at this point. “There is absolutely NO talking.” I look around the room, daring students to even think about speaking out loud without being called on. The students are loving this. They are on pins and needles, waiting to see who might get into trouble. I have transformed into a scowl-wearing, grumbly ogre of a teacher. 

Power of Role-Play

The tension mounts as I walk around the room. I might at this point explain some of the primitive punishments that would have been used during the days of the one-room schoolhouse. It’s not impossible for me to slap a ruler onto a desk to really amp up the mystery of the experience. (Of course, I make certain all of my students understand that corporal punishment is unacceptable in connection with education… but, that is how it was.)

Once I have my students good and primed, it’s time to share the rules of the game. When they are called upon, they are to stand, push in their chair, name the person or persons they are addressing, and make their statement in a complete sentence. I always make it clear that they are to “Refer to me as Mr. Weimann, or Captain Weimann if you’re classy, and you wants to be classy! If you are answering a question, and the information is pertinent for your classmates to pay attention to, you say, ‘Captain Weimann and fellow classmates…’ If there is another adult present, and your answer would benefit that grown up, you say, ‘Captain Weiman, Ms. so and so, peers and/or fellow classmates…’ You get the idea.” We practice this a bit. 

That’s pretty much it. I throw in some variations or additional rules throughout the year to keep the game interesting and fresh. One day I might go crazy about neatness, causing everyone to clean up their desks and the floor around their work spaces. Another day I could go nuts about hearing them breathing. They love it, the more extreme and just beyond grasp the parameters are. A really fun one is pretending to be the mean one-room schoolhouse master and prohibiting all smiling. They practically burst, but work so hard to meet the requirement! 

The trick is to do the game just enough, both in the number of times you play it and how long it lasts. It slows everything down; the making kids stand up, push in chairs, reanswering because they forgot to say who they were talking to or didn’t use a complete sentence. 

This is the tiny bell that turns the room into a “One-Room Schoolhouse.” So little: So powerful!

The students love the game, though. They usually beg me to ring the bell, for I explain that the tiny bell that I got on that very first field trip to the Claussville one-room schoolhouse has magical properties. Whenever I ring it; and only when Mr. Weimann rings it; we are magically transformed into a one-room schoolhouse. This, of course, is a huge part of the game. 

Sometimes, I will pretend to be unhappy with what is happening in the room, and “threaten” to ring the bell. The class will gasp in mock shock. If I do ring it, they all groan and moan, as if they were just strapped into straight jackets against their wills. …But, they quickly sit up straight, quiet down, and see who the big, mean school master from the past will pretend to pick on first. They are always disappointed when we return to the humdrum of contemporary time, and I turn back into fun, loving Mr. Weimann. 

The Claussville One-Room Schoolhouse Bell
What would it feel like to be a student back then?

Back to the Future

This game is like “The Floor is Lava,” in that no one gets hurt, it’s all just pretend, and it amps up the excitement of an otherwise typical walk-through-the-park day. It is perfect for jazzing things up right in the middle of mundane stuff. A little ring of the bell commands everyone’s attention to both behavior and their tasks at hand. 

I had no idea how different the 4th grade class that I was sharing the game with was acting, but their teacher and the accompanying instructional assistant recognized that something unique was going on. Rather than explain the game, myself, I allowed the teacher to call on students, who nearly burst with pride to show off their new skills. 

It took a couple of kids to get all of the rules out, but once I felt comfortable that the teacher understood what was going on, I was free to leave the past. On my way out I whispered, “I’d wait a couple of minutes before ringing that bell. Ride it out;)” 

You don’t want the game to go too long. Fatigue can set in. For the game to be fun, it has to be special, so don’t play it too often or too long. Let the students petition for it a few times, and then surprise them after returning from lunch or in the middle of a multiplication game. Use it for a transition to another lesson. Above all, have fun.

This video shows all three stops of the Polite Pirates’ Lehigh Valley, PA historical sites field trip (2018).

A Bookworm’s Quizzical Poem

I wrote A Bookworm’s Quizzical Poem several years ago. I shared it with my second grade gifted students yesterday when we came across a poem in the book we were reading (365 Penguins).

When I asked them how they knew the poem in the book was poetry, they told me that the letters were fancy. This made me laugh. It reminded me of a blog that I wrote about poetry being intimidating (License to Poetry). While poetry can be beautiful and help you feel fancy, I want to encourage you to guard against reserving it only for ivory towers.

Teaching 3rd grade helped melt my fear of poetry. With an audience of 8 and 9 year-olds, I not only wrote it, but felt free to share and interpret it with my students. I even began to search the Internet for poems that had to do with topics I was teaching in order to deepen my students’ experience during lessons!

As readers of Jack Prelutsky and Shel Silverstein can attest, poetry can be loads of fun to read. It can also be fun to write.

My second grade gifted students and I discussed and explored the rhyming words at the end of each line of the poem from our book. We counted the syllables from each line. The message of the poem was pretty obvious, but it lent to the idea that poetry can be about sharing emotions. Finally, my students and I used the last line to spark a lesson about apostrophes.

They knew that apostrophes show possession, like in the title of my poem, A Bookworm’s Quizzical Poem. And, they understood the concept of showing the missing letters in contractions, but I blew their minds when I told them about poetic license to slice off whole sections of words!

“Why would a poet need to shorten a word?” I prompted. They were quick to identify the trick of squeezing the correct number of syllables into lines. This is when I dug out my old poem.

Did you know that bookworms are real live insects. Back when the glues that bound books were more organic than chemically produced and the pages were pulpier than they are now, larvae would literally feast on the texts.

My poem plays on this idea of a worm eating books, both literally and figuratively. In line 15 the dad says that his son’s book “Was no more than food for my belly.” The next line compares reading a good book to eating something delicious, though.

These comments on the right of the poem are questions that I thought of for helping my students get more out of the text. I ended up typing them into a Google Form to use as a teaching tool. Feel free to use the poetry and form, if you wish.

I always enjoy pointing out the word “shooking” in line 36. It is so silly. It feels weird to say it out loud. After discussing its job of rhyming with “looking” from line 35, I explain to my students that this is a perfect example of me simply having fun with words.

As an author, you have the power and authority to write whatever you want. You can bend the rules. You could even break the rules… a little. If you break them too much, your text won’t make any sense. Just enough, and your writing is interesting, attention-getting, fun, and memorable.

The phoenix’s presence at the end of the poem symbolizes the healing of the relationship between the son and dad, as well as the renewal of ideas. The son will be the next dad. Generations continually move on. Phoenix tears, not that our poem’s bird cried, are supposed to have healing properties.

Also, according to “Ancient Origins” (2021), anyone standing near the pile of ash left when a phoenix burns up can’t help but tell the truth. Is this why the dad confessed to taking the young bookworm’s book? Perhaps it lent to the honesty by which the son told the dad all about his love of poetry and reading.

Whether you love my poem or not, I hope that you open your heart to poetry in general. I have thoroughly enjoyed reading and writing it since I have let go of fears and insecurities.

Here is a video of me reading my poem for my class. I made this during the pandemic when we were all stuck at home, but it also served to differentiate the lesson for students who might have struggled reading. The video is embedded in the Google form so kids can re-experience the poem right before answering the questions.

Buttery Batch of Math Cookies

This is the introduction that I used on my fifth graders.

In preparation for teaching a math enrichment lesson to my fifth graders, I looked at the iReady “Extension” activities in the Ready Math “Teacher Toolbox,” and I found a problem that I liked a lot. (iReady and Ready Math are products of Curriculum Associates. My district has been using it for several years, and I like it a lot.) This lesson (14) is all about using fractions to solve word problems.

Here’s an image of the worksheet that a teacher could photocopy or share via Google classroom. Because I have the luxury of actually teaching enrichment lessons, I decided to do some explaining before handing over the problem. Also, I opted to make a few tweaks, too. In my experience recipes usually call for specific measurements of butter, not a number of “sticks.” Therefore, I covered up the word sticks in the problem and wrote in “cups.”

This changed the outcome of the answer quite a lot. Now, students would not have enough butter to complete the recipe. They could access new sticks of butter, but if they did that, then solving the problem wouldn’t require wrestling with all of the fractions presented in the partial sticks. That’s when I imagined the real-life experience of baking cookies after having worked all day at making a big meal, like Thanksgiving.

Needing soft butter for recipes is a real thing. Also, who doesn’t love consolidating? We can clean up all of those partial sticks of butter and make cookies at the same time!

I shared what a typical day of cooking in preparation for a large Thanksgiving meal looks like at my home with my fifth grade students, setting the stage for having several fractions of sticks hanging around. With the instruction to use up the warm butter first, and then dip into the cold butter from the new package, I set my students loose to calculate how much butter would be left.

Many students jumped on adding up all of the fractions. They began figuring out compatible denominators, so that they could combine every partial stick and find out what they had in all. “But, do you have to do that?” I asked them. No one wanted to venture a guess.

“What are you asked to find?” I pressed.

“Two and half cups of butter,” someone accurately answered. Without saying anything, I drew two of the worst cups ever drawn on an interactive board, followed by half of a third. I made fun of my drawings, which everyone helped with, pitching in their own digs. Once that settled down, I pointed out the lines I’d drawn through the middle of each measuring cup.

“Why’d I do that?” Earlier, we had discussed that fact that one entire stick of butter was the equivalent of half a cup. The students understood better than they could put it into words, so I articulated the concept for them, “Each half of a cup was one stick of butter.”

Then, we looked back at the fractions. It was easy to see that 1 2/3 + 1/3 would be able to fill one whole measuring cup. That leaves us with three fractions with differing denominators. “Before working out a common denominator to add up all three, think about what you are trying to do,” I instructed. “What is your aim?”

I showed the students that 1/2 a stick of butter + two of the 3/4 would equal one whole. “That would take care of half of a measuring cup,” I told them. Also, I should mention that I crossed out halves of measuring cups, as we discovered combinations of partial sticks of butter that would fill them.

“If we used up two of the quarters to combine with the 1/2 a stick and create a whole stick, how many quarters are left?” One quarter. “And then, we have 5/8 of different stick left.”

They instantly got it. We were 1/8 short of a whole stick of butter. In the end we needed one whole cold stick of butter, plus 1/8 of an additional stick to add to all of our warm butter fragmented sticks to fill our two and a half measuring cups.

The Ready Math extension lesson (14) has a second question that I left as is. The catch is that my students used our additional left over cold butter (2 7/8 sticks) from my adapted first problem to solve it. I let them struggle with this one for a few minutes before I showed them the short cut of drawing pictures.

“You might think it childish to draw pictures,” I began. Fifth grade is the oldest grade in my school, so these were the seniors of the place. “…But, I find it easier to manage some problems when I sketch what is happening.” I had been watching them crunching numbers, making common denominators again, and subtracting fractions. Now, within a handful of seconds, I showed them how many quarters could be made from two sticks of butter! I pointed out the idea of labeling the quarters in order to keep track of my thinking. I wrote a B above each “batch” of cookies. Sure, I could just count the quarters, but when it came to the last stick, it will be important to identify what portions of butter will complete a batch.

As I divided the last rectangle into eighths, I asked, “What am I doing to this last stick of butter?”

Rather than answering my question, they were chomping at the bit to be the first to spew the solution to the problem. “Eleven and 1/8!” more than one fifth grader shouted at the same time.

“No, that’s incorrect,” I casually, but cautiously counseled. Rewording what they had yelled in order to make plain the problem with their answer, I said, “You cannot make 11 AND 1/8 batches.” The emphasis on the word “and” did the trick.

“You can make eleven batches, and you’ll have 1/8 of a stick left over,” a student corrected.

“Perfect,” I affirmed. “Drawing pictures might seem silly, but look at how simple it is to see the answer. We didn’t do any denominator work past doubling up the number of sections in the last stick. I hardly did any math, beyond simply counting!

“When you are taking standardized tests, you get scrap paper. Use it. Draw pictures. Illustrate word problems. Take the time to label parts of your illustrations. Make sure that you understand what you are being asked. What is your goal? What are you supposed to find? It’s not just a number. It is the solution to a problem. In real life, it is a key that will unlock a problem. Be a problem-solver; Not a human-calculator,” I told them.

Photo by Elliot Fais on Pexels.com

In conclusion, my aim is to turn these advanced math performers into problem-solvers. With this goal in mind, I try to make lessons that force students to use what they have learned in their regular math class in a way that is not only compatible with what they would find in the “real world,” but forces them to understand how to use the skills. I often allow my students to use calculators because the problems I prepare for them require more knowing what to do with the numbers than practicing running through algorithms. AI can learn how to crunch numbers, but will it be able to successfully manage a kitchen full of amateur chefs laughing, telling stories, and making meaningful memories, all the while measuring butter for cookies after already cooking and eating a Thanksgiving dinner?

To combat the threat of AI, don’t try to make humans better than machines. That just makes them more like machines. I say, grow the human-ness of students. This is getting pretty deep, so I’m going to go eat a buttery cookie while I chew on these ideas for a future blog;)

Nemesis Brings Balance: A Story

In preparation for teaching my 4th and 5th graders about conflict in literature, I did some research that uncovered something novel. I had always thought that someone’s nemesis was the antagonist of the story, the enemy, the ultra-bad guy, the anti-hero. This isn’t exactly the case. Before I share what I learned, I have a story for you.

Photo by Steshka Willems on Pexels.com

There once was a baseball player born with a natural affinity for the game. It was more than that. He had a gift. His parents knew he would be great, and they gave him everything he would need to fulfill his destiny. 

Everyone who saw this boy play commented on his skills. When he threw the ball it seemed to know where it was supposed to go. His glove was a magnet. No toss escaped it. The bat in his hands may as well be Thor’s hammer, Mjolner. It punished pitchers year in and year out. 

A funny thing happened early in the boy’s career. He was still in school when a coach who understood the greatness before him told the ballplayer’s parents, this one will go far as long as he never assumes his talents, but continues to practice and better himself. This coach had glimpsed raw talent before, and knew that without tuning, the song of the marvelous instrument turns into a grating noise. 

The young baseball player had no problem making it to the big leagues. The people who played ball with him were graced to know his genius for the game. Even his opponents felt privileged to have been able to rival him. 

Numerous articles were written about the rising star. Every journalist craved an interview with the boy, but he eluded them all. One journalist in particular resolved to take photographs of the athlete in action. If she wasn’t granted the privilege of speaking with the ball player, she would communicate his greatness to the world through picture. 

The journalist, not new to baseball, had never seen the human body move the way this star player moved. Her photographs captured the power of the throw like none other. Looking at the glove that never missed a toss portrayed in portrait amazed every viewer. 

Even though no one secured an audience with the baseball player, this photographer wished to put words to her photos and sought an interview. Rejection after rejection caused the journalist to turn to other means of query. She would write letters to the baseball player. She tried to get his manager to intervene. The journalist befriended other players in hopes that they would put in a good word for her. Eventually, the journalist even bought presents to give to the baseball player. Perhaps she could bribe him to give her some sound bites, at least. 

Other journalists saw this photographer pining for the privilege to interview the star as pathetic at first. They feared the photographer would fall apart, focusing so much attention on one person. They warned her. It was too late. And then, she was gone. 

Photo by Tim Eiden on Pexels.com

The owner of the magazine that the photographer worked for heard the speeches of brother and sister journalists at the photographer’s funeral and decided to do something about this tragedy. Why wouldn’t the baseball player just talk to his employee?

The magazine owner compiled a book of the best photographs and had it delivered to the baseball player. There were no words. Not even a title was printed on the cover! Everyone knew who was featured in the photos. It didn’t take much research to find out who had captured the pics. 

What no one foresaw, though, was the way in which the photos would imprison the baseball star. He had never bothered to read the newspaper articles written about him. He hadn’t ever seen the famous photos. When he viewed the pictures of his playing, he was mesmerized. Is that how he looked to others? 

Photo by Lisa Fotios on Pexels.com

He removed photos from the book. Framed his favorites. They were placed all over his house. He found it difficult to pass one without stopping to look. Eventually, the baseball player couldn’t leave his home without missing the photos. After a while, he stopped leaving all together. 

The once great star didn’t eat. He didn’t drink. He wasted away to nothing. When his friends went to check in on him, they didn’t find a former baseball player. All that was left was a flower; A daffodil. 

Did you recognize my modern myth for what it was, a retelling of Narcissus? I wrote this version for my students. I wanted to emphasize the idea of undeserved good fortune, a theme I had overlooked in the past. 

More than rivaling a hero, Nemesis is a “balancer of the scales.” I’ve thought that Nemesis was synonymous with antagonist, but she isn’t. I didn’t remember her role in the Narcissus myth, but she was the one who led Narcissus to the pool where he first beheld his reflection. She heard the prayers of the nymph-friends of Echo, who died of unrequited love. 

I always focused on Narcissus getting what he deserved, but there is much more to the original story. First of all, his parents had been warned that Narcissus would live long if he never knew himself. I wove that into my tale by having the baseball star’s coach warn against relying too much on good luck and gifts. Talents need to be honed, stretched, developed. 

Next, I never recognized the role of Nemesis in the story! She deliberately brings Narcissus to the pool where his downfall takes place. She knows the prophecy. She understands the importance of Narcissus remaining ignorant of his beauty.

It isn’t pay-back, though, that drives her to initiate Narcissus’s learning about his looks. It is a need for balance. Nature was too kind to Narcissus, just as my baseball player was too talented. In my tale, the magazine editor brought balance by making the athlete see the photos that the gifted photographer captured. I hope you recognized the photos for what they were; “Echoes” of the action.

Wallpaper Based Learning: Math Enrichment

Who wants to see a picture of Mr. Weimann with hair?

EVERYONE, apparently. I used this hook to get students to pay attention to my pitch of wallpaper hanging. They hung on my every word. 

This was a math enrichment lesson, in which I presented a real world problem that my fourth grade advanced math students would struggle through, using many math concepts that they already know. Knowing what to do with the numbers is sometimes more than half of the problem.

When I was in college (the first time;), I began painting to pay my way. Back then, it was just the outside of homes (exterior painting). Upon graduating, I conducted an informal internship with a wallpaper hanger. He taught me all about interior painting; which is VERY different from slapping paint on siding; and he trained me to hang wallpaper. 

This pic is from 20 years ago.

I was 22 years old, had long, curly, brown hair, and according to my students who did end up earning the privilege of viewing my old photos, quite tan (nearly all of them commented on this fact;). I worked with the professional wallpaper hanger for a little less than a year, hanging all kinds of paper in all kinds of homes. 

About half of his work came from a restoration company that did insurance projects. These homes had suffered water, smoke, or fire damage.

Unlike a company that specializes in a niche of upper-middle class single family repaints, this work brought us into a wide range of residences. I worked in downtown Philadelphia and on the Main Line, a very wealthy area–This place has both Ferrari and Lamborghini dealerships, among others!

This was one of the stranger bathrooms I papered. I had to paper inside that skylight.

We rehung thick, tough paper on basement ceilings; and metallic, mirror-backed papers in tiny bathrooms. It wasn’t unheard of for me to have to remove several layers of paper in older homes, in order to get to a clean plaster surface. 

It was fun to see so many different types of homes, meet a variety of peoples, and travel all over the area. I learned a lot about problem-solving because every job was completely different, and you didn’t get paid until it was done, and done well. 

Eventually, I struck out on my own. I got married in 2000, and my wife Sonia and I started our own painting company called “Excellent Painting.”

We used feathers to produce the veins on this marbleized pillar.

We ordered lawn signs and door hangers, spread the word, and pioneered a full-service painting/wallpaper business that did it all! We even dabbled in faux finishes, popular at the time. Faux finish is when you use tricks and artistic techniques to make pillars and walls look like marble, stone, or wood.

Because we were the only company that could do all three, we got a lot of business, especially in the new developments that were popping up in suburban areas near where we lived. The market was ripe, and we were busy. 

This is a photo of one of our neighborhoods. We would literally move our equipment from one house to the next, working our way around the loop. Having the interior of your home decorated by Matt and Sonia Weimann was a must.

There are many components to running a successful business. You have to market the company, spreading the word, so that people know to call you. Then you need to return phone calls and perform estimates. Those estimates need to be cheap enough that people will hire you, but expensive enough to cover the costs of supplies and provide a livable income.

Eventually, you have to deliver on your promises. You have to be able to successfully perform the work that you estimated. Be prepared to follow up on complaints, questions, and problems. If you don’t, an infection of bad publicity will spread around the neighborhood, and you can write that group of homes off! Do things well, and reap the rewards of moving from house to house, cutting down on marketing costs and time. 

This is an advertisement from a small local paper that was mailed to many homes in our area. It was an awesome investment!

Many of the skills and lessons that I learned through entrepreneurship are tapped in my teaching. Some days the professional world mixes with pedagogical practice more than others. My favorite place to bring my background to life is in math lessons. 

The other day, I treated my fourth grade math enrichment class to a treat of problem-solving that had them working hard, thinking hard, and learning hard. The challenge was to help me come up with a price for wallpapering a couple of bathrooms.

I shared a photo of a bathroom that I papered several years ago. Many opinions about the bathroom were unsolicitedly shared by my students. In order to get them motivated, I asked, “Who wants to see a picture of Mr. Weimann (that’s me;) with hair?”

Instant quiet. Hands involuntarily went to mouths to clamp lips shut.

“Listen up.” I proceeded to explain that you don’t just glue wallpaper to walls. You have to perform all kinds of preparatory work. 

There’s taking down old paper, because many times the rooms that you are going to hang wallpaper in were rooms that were already wallpapered. This is a lot of work. You may not know this, but wallpaper is two layers. There is the thin vinyl layer that sometimes peels off in large flexible sheets, but other times has to be slowly, painstakingly, curse-your-existence-ly chiseled off of the walls in tiny, bitesize pieces; As, you can probably tell, I have had too many experiences like this! Then there is the backing, which more closely resembles actual paper. This, you wet and scrape off rather nicely. There are all kinds of tricks to removing wallpaper more efficiently, but suffice to say, you better estimate plenty of time for this part of your project!

Sometimes I used a steamer. Other times you can just spray warm ammonia water on the wallpaper.
More often than not, you just chisel away at the top layer.

You aren’t done preparing the walls for wallpaper when all of the old paper is removed, however. Before you move on, you have to clean off all of the old glue! If you don’t, your new paper may not adhere properly. You do not want your new wallpaper to fall off the walls or bubble up. This process is not only messy. It can be deceiving. The glue is transparent, so that it does not discolor the wallpaper. Cleaning it off of the walls requires diligent and frequent assessments. Run your fingers over a cleaned wall. If you feel anything slippery or slimy, it is probably glue that still needs to be scrubbed off.

People don’t hang wallpaper the way they used to. My students will probably never practice this skill. But, I shared all of this information with them, so that they could see that there is much more to crafts like this than what meets the eye.

Once my students had been prepped with the horrors of wallpaper work, I brought out some numbers. I kept it simple with easy fractions to work with.

We would charge one whole dollar per square foot for actually hanging up the wallpaper, ½ a dollar for taking down the old wallpaper (Once in a while rooms don’t have wallpaper to remove. Plus, you want to make this a separate price so that customers appreciate all of your hard work, and it doesn’t seem overpriced.), and ¼ of a dollar per square foot for prep work. (This would include cleaning the walls, caulking cracks, and spackling holes and other imperfections that the paper won’t hide.) These prices are from when I was first starting out. I actually did this kind of thing, regularly.

Next, I shared a simple floor plan with my students. Some of them recognized the blueprint for what it was. I showed them the illustration of doors and asked them what the rectangle representing a closet was. We discussed what was happening in the picture for a minute. And then, I told them that our customer wants to wallpaper the two bathrooms. 

The image was presented on an interactive Google Jamboard, so I could write on the board. I used a bright blue to rewrite the dimensions of the bathrooms in question. I told them that the ceilings were 8 feet high. When I turned around, I was met with incredulous faces. They had no idea what to do!

This was perfect, because it provided me an opportunity to teach. I told them that a good strategy when dealing with a difficult problem is to draw pictures. I drew four rectangles beside the image of the floor plan on the Jamboard. With a little prompting I got my fourth graders to figure out that we would need to find the square footage of the wall space that would be covered with wallpaper in order to create prices. “What are these four rectangles?” I asked. 

I’ll confess that the first time I did this lesson (I have an AM and a PM 4th grade math enrichment class) I tried drawing a three-dimensional image of the bathroom on the side of the floor plan, and this ended up being too difficult to understand. I ended up pulling each wall from my drawing out and making individual rectangle representations.

In my second attempt, I cut straight to the 4 walls. This was less confusing.

Either way, it required some spacial thinking to understand what to do with the numbers.
This was my first (AM) lesson.

Once it was established that my picture of 4 rectangles were in fact the walls, we labeled the dimensions: Each one was eight feet high, and two were one length, while the other two were a different length. 

In order to figure out the square footage of all of the walls, you solve the area of each, and add them together. This reads simple enough, but my students had never had to do anything like this before! 

It took a little convincing to show them why we needed the square footage at all. I used the dimensions of our classroom and kept it to only one surface; the floor.

“How big do you think our room is?” I prompted. After a couple of guesses, I told them that I thought it was about 30 by 15. I then paced out the floor and found it to be 11 paces by 6 paces. “If we calculate each pace to be worth 3 linear feet, what are the actual dimensions of the room?” Wait for it. My students knew to multiply 3 times 11 and 6, respectively.

“Are 30 and 15 easier to work with?” 

We used the dimensions of our classroom floor to practice. (The -100 was subtracting the cost of supplies.)

“They are compatible numbers,” Evie answered. I beamed with pride. We’ve been talking about using helpful numbers to do mental math a lot.

“That’s right; Much easier to work with. And, what is 30 times 15?” Blank stares. “What is three times 15?” Now we were thinking! When we figured out the answer to that, I wrote “15 X 3 X 10” on the Jamboard. “Thirty feels big, but pull it apart. It’s just 3 tens.” 

“So we know that the floor of the classroom is about 450 square feet. How much would it cost to wallpaper the floor… Of course no one would do this, but what would it cost?” Everyone quickly understood that it would cost $450, since each square foot would cost one dollar. 

“Now, let’s say that some maniac had already wallpapered the floor before we were asked to. What?! Crazy, I know, but what if… We would have to remove that old paper before we can apply any new paper. How much will that cost? It’s fifty cents per square foot,” I remind them. It doesn’t take long to figure out half of 450. 

“And, finally, there will be some prep work before actually wallpapering. That costs twenty-five cents per square foot.”

In order to illustrate this concept, I drew a square on a new, fresh Jamboard slide. I labeled it $1. Then I drew another square, the same size as the first, and drew a line down the middle. I labeled each half $.50. Before going any farther, my math enrichment students knew to halve the half. 

While a couple of kids knew what to do with the twenty five from $225, some didn’t. I told them to break apart the number. “Don’t think of it as 225. What is half of two hundred?” I wrote 100 on the board when they said it aloud. “What’s half of 25? How do you know that it’s 12 and a ½?” 

Evie-to-the-rescue-again explained that 24 divided by 2 is 12. The one extra that it takes to make it 25 can be split in half. “Nice,” I encouraged.

“So, how much would it cost to do the whole project on the floor of the classroom, provided some nut wanted to wallpaper a floor?” Staring students looked stunned. “You have the price for applying the wallpaper,” I said, circling the $450. “You have the price for removing the old wallpaper.” At that point, I circled the $225. “And, we just figured out that it would cost 112 and ½ of a dollar to prep the surface.” 

“Do we add it all up?” a hesitant student asked. 

“That’s right,” I said, trying to sound proud and hoping to steer my students toward feeling like they can do this. “Now, time to figure out what this bathroom would cost!”

I let them struggle a little before helping. They needed a bit of guidance. But, we figured out the square footage of all four walls. They did pretty good finding out what it would cost. And, the second bathroom was a little easier. 

A funny experience happened at the very end of the afternoon lesson. This PM group of fourth graders originally entered the room with the announcement that they already knew the answer to the problem.

A couple of them had walked in on me finishing up my morning math enrichment lesson. They confessed that they already knew the final answer to be $952, “or something.” 

I told them that I was going to change all of the numbers, so it will be different. They thought that sounded reasonable;)

I had intended to make the ceilings 9 feet tall for the PM class, but the concepts were difficult enough to understand that I didn’t feel like it was all that necessary. But, by the very end of the afternoon lesson, after I told the students to take the prices of the two bathrooms and add them together so that we can tell the customer how much it will cost… 

“Wait,” they exclaimed. “You didn’t change the numbers!” Huge smiles stretched across their faces. They loved being tricked.

“Look at that. You ended up needing to do all of the work, anyway.” We all laughed as they exited the room. 

Communicating Creative Mental Math Verbally

“I don’t know how I got it; I just know that this is the answer,” a frustrated student defends himself against the inquisition of an even more frustrated teacher who wants him to “SHOW YOUR WORK!”

You should have seen the students’ eyes bulge when I told them I was going to give them candy! LOL They were happy to gobble up the math, though.

But, what if he actually doesn’t know where the number came from? We don’t ask the toaster to “Show us how it heats up our bread.” When was the last time you insisted that the mechanic “Show you HOW they fixed your car”? (They always try to explain it to us, and I’m like, “Does it work? How much does it cost? I got stuff to do.” Ha ha;)

I recently had a math enrichment lesson with second graders where I told them what they didn’t know they did with a couple of mental math problems. We were working on comparing three-digit numbers. I had printed pictures of snacks that had prices on them. Teams of students were first asked to arrange the snacks in order from least to greatest price. Then I asked the class to compare the cost of three items to the cost of two others. The students didn’t have paper or anything to write on. 

Please pardon my penmanship;)

After I received some successful answers, I asked the teams, “What did you do in order to produce those answers?” I got a variety of responses. Most teams told me the names of the operations. “We added the three numbers together, and then subtracted…”

One group explained what they did to complete the operations, and I was very impressed. While students were sharing, I took some notes on the board. I clarified what the group was communicating by drawing circles around numbers and pulling out concepts.

“You began by adding 65 cents to 55 cents,” I reiterated. Nods of heads confirmed the accuracy of my statement. What happens in a creative mathematician’s head is a little different from what one would do on paper, however, and I wanted to pull this out. These students hadn’t used an algorithm.

I like to do a lot of mental math in my room, because it helps kids develop number sense. “The 65 and 55 are both pretty close to a number that is really easy to add in your heads,” I told them.

Here’s a post that shows 3rd graders communicating the use of compatible numbers to multiply.

“Fifty!” the group called out. We have been identifying compatible numbers, so they already knew to look for something more manageable.

“That’s right. And, in order to get to fifty, you have to adjust these a little.” I circled the 65 and wrote 15 on the side. Then I circled only the 5 from the ones of 55, and I wrote that near the 15.

If a student had paper in front of them, they might line up 65 and 55. Then they’d add the fives from the ones’ column and regroup with a “one” above the tens column… But, do we grown ups do this in the grocery store when we are comparing one item with another? No, we use mental math. We develop creative tricks that we may not even realize we use!

My aim is to unlock this mathematical creativity early in life. A secondary goal is to help students be able to communicate it.

“After adding the two 50s together, what did you do?” Everyone can see that there is still a 15 and a 5 written on the board. I wrote the sum before anyone called out, answering the rhetorical statement myself. “Now, you need to add this $1.20 to 99 cents. That sounds hard,” I teased, knowing that they’d already smashed that algorithm in their minds.

Letting students work in teams allows them more than just Social Emotional Learning (SEL). They help one another remember and recall sums and differences.

When I told them about using 100 instead of 99, several students silently shouted, “That’s what I did!” No one is going to carry a one from the tens to the hundreds column of a mentally constructed algorithm. And, we don’t always have paper. AND, do you really want to teach your students to be dependent on paper?!

Now, think about it, reader. Students are using subtraction in order to add numbers together. What 8 year old is going to be able to explain this abstract use of arithmetic in writing on a test or assessment?

Here, I’m having the group of 2nd graders “play” with numbers by lining their teams up in order of least to greatest, having constructed the largest number possible with the loose number cards I’d given everyone in each team. Get-up-and-move-around-math.

And, we (myself included) expect them to “Show their work!” I’m happy if they know what they are doing and get the correct answer. I’m nearly 50, and I only just learned how to show MY own work! LOL

What I found myself doing in the past was asking students who had performed mental gymnastics to achieve a remarkable mathematical feat to write down the steps they took. In other words, if you added up three numbers (65 + 55 + 99), and then subtracted a fourth from that sum, write it all down…

Even if you can’t describe the exact process of creating the sum or exactly what you did to subtract. Just tell me what you did with the numbers. I, like every other math teacher in the world, wanted to see more than just an answer!

I think that having students use mental math, and then having them explain what they did VERBALLY is helpful in sharing the mechanics of the creative math. It’s easier to verbalize than it is to write. I bet there are books written about this. (If you know of any, please share. Thank you.)

A tool I’ve enjoyed having students use to verbally communicate their creative math skills is Flip (formally known as Flipgrid). Kids can make videos of themselves talking about the math. They can also write on their screens to show what they did while talking about it. If they did the math on paper, they can take a photo of their work to include in their video. Finally, they can watch each other’s videos, get ideas for future creative math projects, and leave encouraging replies to each other. The platform is easy to navigate and teacher-friendly for leaving feedback and assessment info.

In conclusion, while I always instinctually knew that forcing a kid to write down everything they did in their head could squash their creativity, I never knew how to bridge the gap between teacher and student; The chasm between the answer (what the student produces) and the process (what the teacher cares most about) before now. I’d tried varying techniques with varying results. My new thing is to verbally walk them through tricks I’d use to do mental math. Through this process, they recognize some of what they are already doing in their minds. They are learning how to communicate it. And, some students are learning creative ways to play with numbers.

Give Your Teaching Life by Using Real-Life Situations to Teach

It’s math enrichment time again. The pacing guide has the fifth graders learning to add and subtract fractions. Our curriculum has an enrichment lesson that students can work on independently. It’s a grid that has empty spaces that need to be filled in order to help every row and column add up to the same sum. I like these types of exercises because they are puzzles and make the practice feel like a game. 

This is the enrichment activity provided by iReady. It’s a good tool for independent practice, but I wanted to provide a “Math Experience.”

I view my job as a math enrichment educator as deepening the understanding of already mastered math skills. Puzzles and games are a great way to make the skills easier to access, faster to use, and more accurate. They are excellent tools for regular ed teachers to provide for those students who have demonstrated competency in a math concept. This style of enrichment activity is good for keeping the advanced students busy while the teacher catches everyone else up to speed. For my part, I aim at helping students see the math from a different perspective, though. 

I cut all of the tiles for the ceiling before attaching them.

It makes a grid of mixed numbers!

Diamonds are beautiful, rare, and expensive gems used to make jewelry, but did you know that they are also the hardest substance on Earth? In fact, the fragments that are cut away from a diamond when it is shaped for a piece of jewelry were used to make saws and drill-bits that can cut through rock (2023). I’ve had the experience recently of using a diamond-studded saw blade to cut through ceramic tile and marble to make a new shower in my house. Just like adding and subtracting fractions can be used to complete a pretty grid, they are also very useful in everyday life. I hoped to make my students’ understanding of fractions more rich (enriched) by having them use their skills to help me measure tile precisely. 

This was one of the most difficult home remodeling projects I’ve tackled. I should use it to teach my students, I thought to myself. So I did.

Welcome to math-enrichment, real-world experience-mode. This project was full of fractions–really! I was excited to share it with my students. 

The first thing I did was think about the different ways I had to work with fractions in order to make the ceramic tiles fit my shower walls. I came up with a math problem that involved quite a lot of fraction work. This will be good, I thought, but perhaps there’s a simpler one to begin with. Even though it’s not the first part of tiling, I decided to have my students measure the window sill, a piece of white marble that had to be exact because the sides of the frame were already tiled. 

I put a photo of my window, minus the sill, into a Google jamboard. The photo shows my tape measure. “I took this picture, so that I would remember the exact measurement when I was at the granite store ordering my marble. I don’t want the gap to be too big on either side of the marble, or it will look weird,” I tell my students. “What I want is for the gap to be the same size as all of the other gaps between tile in the shower, ⅛ of an inch.” After explaining the parameters of the problem, my students have a goal: Make the marble look nice. It will look nice if the measurement is just right. “The space we have to fill is exactly 28 ½ inches wide,” I informed my students. “What width will the marble be cut in order to leave ⅛ of an inch on either side? Go!”

Anyone with experience measuring with rulers and tape measures for cutting materials will understand that you can simply back up your finger or the material on the tool to find the answer. Fifth graders have not had this experience, yet. Also, we were sitting in a classroom, instead of holding a tape measure up to the empty window frame.

After letting my students wrestle with the fractions for a few minutes with a couple of them finding success, I showed the class how to look at the problem, by holding up a yardstick. I placed my finger at the 28 ½ inch mark. I slid my finger over a fraction (⅛) of an inch and asked them how much I just “cut” off of the marble. They saw that it shrank by ⅛ of an inch. “Now, we need to take ⅛ of an inch off of the other side, but do we move our finger ⅛ of an inch from the beginning of the yardstick?” I paused to let them imagine what would happen if we did that. “No, we include the subtraction of that ⅛ of an inch right here,” and I slid my finger over another fraction (⅛) of an inch. “Now, how wide is our marble?” 

Some of my students had written 28 and 2/8 on their papers. When we looked at the yardstick together, we discussed that it is better to say 28 and ¼ of an inch… “Not just because you are supposed to reduce your fractions! But, because one is easier and faster to count than two; plain and simple.” This set us up for our next problem, the one I had come up with originally, but put off until after having practiced some measuring, first. 

Time for some tiling!

“Now, we need to cut some ceramic tile to fit my shower wall,” I pitched. “Remember, we want to keep gaps of ⅛ of an inch between everything; between the tile, between the corner of the wall and the tile, between the tile and the metal edging; everything.” (This isn’t just easy for students to forget. It is easy for someone measuring for actually tiling a shower to forget. I should know! I can’t tell you how many times I had to re-measure or recalculate because I forgot to account for the grout!) 

“Okay, so our wall is exactly 30 and ¾ inches wide, from the corner of the shower to the metal edging. I’ve already tiled the window wall,” I explained. “This 30 and ¾ inches is the space that we need to fill with tile and grout.” I showed them a tile and told them that it is two feet by one foot, rectangular. There was a photo of my shower wall in the Jamboard, too. I wanted them to visualize the final product. While I had written the entire problem into a Google jamboard, I shared the problem with them orally, also. It was easy for me to communicate, because I just did this! It was fresh on my brain. 

“We will be alternating the tile,” I told them. “We begin at the bottom of the shower wall and work our way up. The first row will begin with a whole piece of tile placed in the corner. The next row will begin with half of a tile starting at the corner, and so on.”

Surprise! The tile isn’t really 2 feet by 1 foot; not exactly.

“Guess what,” I exclaimed. “I have a treat for you: The tile that you thought (I thought;) was two feet wide isn’t! Like everything else in life, it is a little short; a quarter of an inch short to be precise. It’s your job to figure out exactly how wide to cut the tile that will fill the gap that is left within the 30 ¾ inches space. Don’t forget about the ⅛ inch grout between everything! Go.” 

Student mouths hung slack-jawed. I used the Jamboard to demonstrate the math. I drew lines that represented the sides of the shower wall. “This is the corner,” I told them, pointing to the line on the right. “And, this is the metal edging that is the end of our tiling.” I pointed at the line on the left when I said this. “Now, how wide is the space between the two lines?” I prompted. 

It took some waiting, but finally one of the students ventured, “Thirty inches?” 

“Thirty and what?” I reminded them.

“Three quarters of an inch,” they completed. I told my students that this was the width of my tub (30 ¾ inches).

“Okay,” and I wrote the complete distance in the space between the two lines. “Now, let’s begin by allocating ⅛ of an inch over here.” I drew a little circle next to the line that represented the corner. “What comes after the ⅛ inch of grout?” Pause. Wait. Patiently persist in waiting. “Look back at the problem.”

“A tile,” someone says out loud.

“Yes,” I affirm the correct answer. “We put a whole tile on the wall. How much distance does that take up?” I went ahead and wrote on the Jamboard while they were thinking: 24” – ¼ of an inch.

“23 and ¾ of an inch,” a student answered before I was done writing. Pleased, I put the length into the designated space in our row of tile. 

“Now what?” I asked.

“We figure out how wide the remaining space is,” a student said in a half statement/half question.

“Yes, but…” I wanted to provide positivity, but needed to help them toward accuracy. “Don’t forget about the ⅛ of an inch on either side of the remaining tile. You have to leave space (⅛”) between the two pieces of tile and also a space (⅛”) over here.” I drew tiny circles and labeled them on the Jamboard. “Use all of these measurements to figure out where I will cut my tile to place on the wall,” I told them. “Be careful!” I warned. “I don’t want to waste any tile. I have just enough.”

There were a few ways to figure out the answer. You could add up all of the fractions. And then, subtract the mixed number from 30 ¾ inches. You could also subtract each individual “space” away from 30 ¾ inches to see what is left. This method is like sliding your finger down the yardstick. After letting the students try the math on their own, we discussed. 

If you thought that the previous problems were difficult, buckle up. “Now, I have a real treat for you,” I told my students. “That first whole tile; The almost two feet wide tile; We have to cut a hole in it. The spout for my tub has to go through it.” Groans. “That’s right! I want the pipe, which is exactly one inch in diameter, to be in the center of my wall. What does that mean?”

“Halfway,” someone says. 

“Yes.” I let that sink in. “How far from the corner is the pipe?”

One of my fraction experts quickly tells me that it ought to be placed 15 ⅜ inches from the corner. I was pretty impressed, and had the student explain how he had converted ¾ into 6/8 in order to divide the fraction in half. 

“That’s right, but that is the center of the pipe,” I tell them. After explaining the term diameter, I point out that half of an inch will be on one side of 15 and ⅜ and half an inch on the other. “Where do we cut the hole for the pipe? …Don’t mess up! We don’t want to waste a great big whole tile!!”

After they fight with fractions for a minute, I remind them of the ⅛ inch of grout that precedes the beginning of the whole tile. Many groans follow this reminder. 

The whole lesson ends with me warning the students that, “After all of that measuring and math, you better be sure to cut the tile on the correct side of the line you draw, because your diamond blade will shave 1/16 of an inch off of whatever you’re cutting. In other words, you could figure out that the hole for your pipe has to be cut 14 ⅞ from the edge. Mark that measurement on your tile. And then, when you go to make the cut, slice the tile on the wrong side of the mark, which would make the distance from the hole to the edge of the tile 1/16 of an inch short. What would that be?” I posed the question, but didn’t actually expect them to figure it out. They knew I was messing with them, and they all gathered their things to leave. 

“Wait! What about our next row of tile?” I laughed as they left shaking their heads. 

Tony Wagner, the author of “Creating Innovators: The making of young people who will change the world” (2012), describes the practices of some highly effective schools. One of them is Olin College, a small engineering school that is pioneering hands-on learning.

“In classes at Olin, the primary goal is not the acquisition of knowledge. The goal is to develop a set of skills–or, in Jon Stolk’s terms, competencies–by solving a problem, creating a product, or generating a new understanding. Knowledge is important, but it is acquired on an “as needed” basis. It is a means to an end. Traditional academics often criticize this approach for being too utilitarian and lacking an appreciation of learning for its own sake, but the evidence is that Olin students are very well prepared for graduate school and better prepared for work, with managers who have been surveyed by the college reporting that Olin students who’ve just graduated act as if they’ve had three to five years of experience. Learning research shows that students understand and retain much more of what they learn when they have studied and used the knowledge in an applied context.” (Wagner, p. 175)

“When will we ever use this in real life?” is a question many math students will utter when trudging through seemingly pointless pedagogy. Infuse life into your teaching by showing how the lessons are used in real-life.  

Sources:

Development History of the Notched Rim Lapidary Diamond Blade. Barranca Diamond. (2023). https://www.barrancadiamond.com/home/history.html#:~:text=Richard%20Felker%2C%20a%20pharmacist%20develops,natural%20and%20manmade%20stone%20products.  

Wagner T. & Compton R. A. (2012). Creating innovators : the making of young people who will change the world (1st Scribner hardcover). Scribner.