Tag: mathematics

Show Your (Math) Work (Part 2)

Algebraic notation in chess shows each move that a player makes. Ranks (rows) are notated with numbers, while files (columns) are designated a letter. Thus each of the 64 squares on a chess board has a name, the letter first, followed by the number. For example, the most popular opening in a game of chess is to place a pawn on the square e4. This square is located within the “e” file and on the fourth rank.

Chessgames.com provides the algebraic notation, along with some commentary, for “The Game of the Century.”

In order to show what happened during a chess move players write down not only the square that a piece was moved to, but also what piece was moved and whether something was captured, checked, or checkmated. (There are a couple of other symbols, but these are the major ones.) Abbreviations are used in order to save time. The moves are recorded so that the game can be analyzed and studied afterward. Most chess apps online and on phones will create the notation for you.

The algebraic notation of a chess game looks a lot like code. That’s because it IS! It is a string of commands. If you know how to read it, you could recreate a chess game, move by move. You could plug the code into a computer, as chessgames.com did for “The Game of the Century” between 13 year old Bobby Fischer and International Chess Master Donald Byrne originally played during the Rosenwald Memorial Tournament in New York City, October 17, 1956. 

For several years I have been teaching elementary-age kids (7-11) how to play chess. I’ve run a chess club that meets after school. While I always share information about how to read algebraic notation, I don’t require them to use it during play. I want them to learn the game and have fun. 

As students get better and begin playing in tournaments, however, they will need to learn to use notation. During competitive play, they will be required to write down the code for each move on a piece of paper. Next to their move, they will also write down their opponent’s moves. In this way, they will be able to “view” the game after its completion. Serious players do this to evaluate each move. Which ones were better than others? Where did I or my opponent falter? What was the critical move? What could I have done differently? 

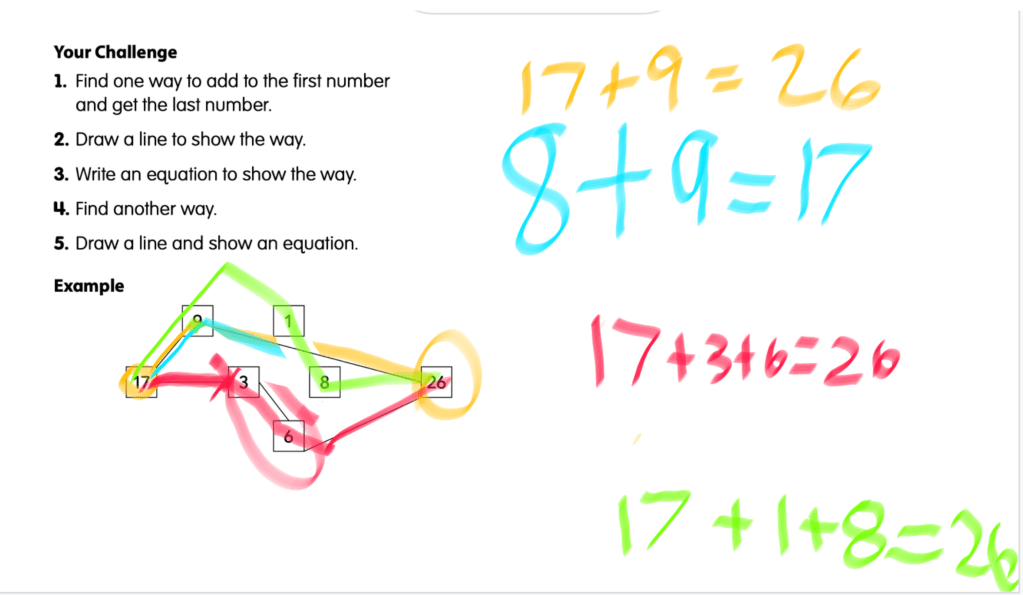
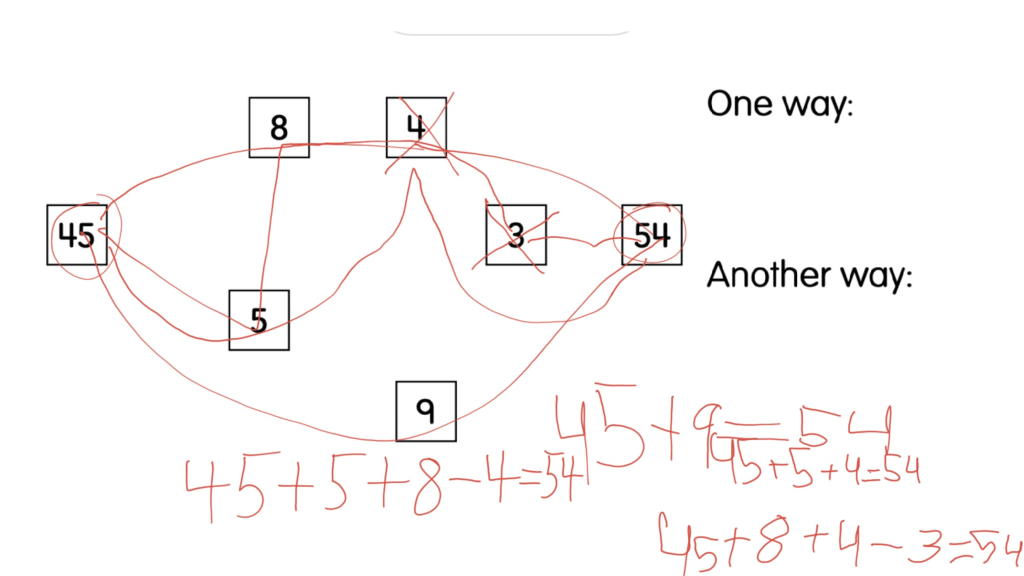
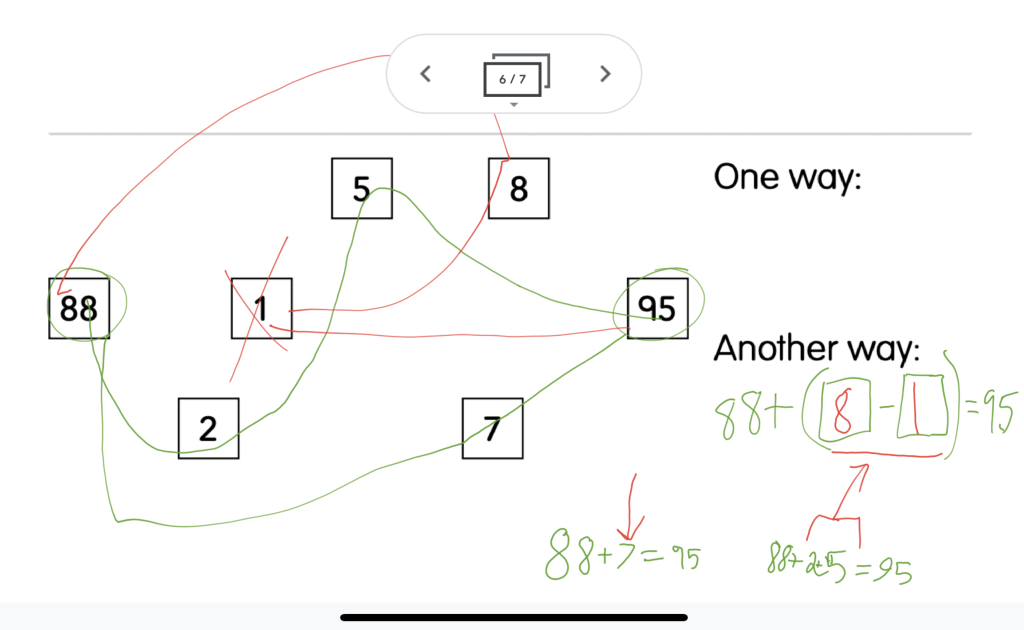
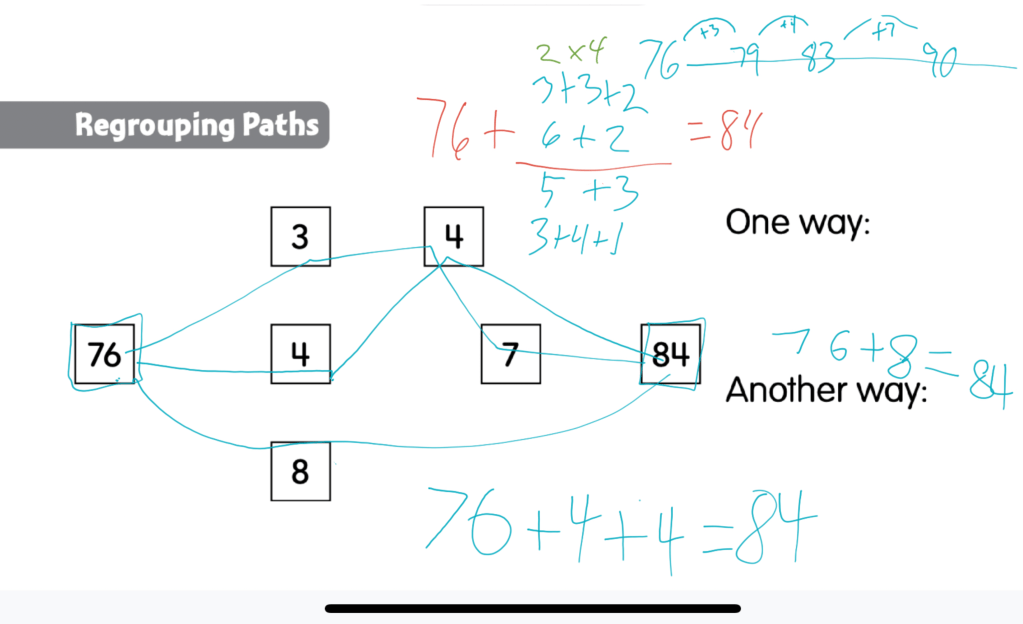
When solving a math problem, it can be valuable to write down some notes. Why? Sometimes you do this to keep short term memory space available. If there are a lot of numbers and a lot of computation is going on, there might be too much to remember in your head. Along the route of figuring out the answer, you write down what you have so far. 

Another reason for taking notes can be showing the steps you took to solve the problem. This might help someone else see a path from beginning to end of the math problem, demonstrating how the answer was achieved. They could “replay” the action of solving the problem by reading the steps taken.

In school, this last “reason” is usually proposed by teachers who want to “see” how you did your work. They say, “Show me your work,” so often that it becomes grating. And, writing down each step of computation can become tedious for a student who just knows the answer. Back in January (2024) I wrote a blog (Part 1) about students communicating their math work creatively. Learning to write down the steps involved in solving a math problem has value, however.

Here are a couple of ideas.

First, instruct students to treat each math problem as though it were a rock-climbing problem. Ashima Shiraishi is a champion of solving problems. She wrote a book about it. “How to Solve a Problem: The Rise (and Falls) of a Rock Climbing Champion” tells the story of 13 year old Ashima figuring out a map that will guide her to the top of Golden Shadow, a V14 boulder in Rocklands, South Africa. The story is an excellent metaphor for not giving up. It also shows how Ashima uses imagery to map out a doable path up the face of a difficult climb. She assigns symbols to the holds and footings that she uses. As she ascends, time after time, for it takes many tries to successfully conquer a difficult problem, she creates a story in her head, using the beneficial symbols (holds), so that she can find her way. The book, illustrated by Yao Xiao, shows (on paper) what Ashima does in her head. 

I often see students erase their math when they have tried a set of steps that did not accurately solve a problem. “Don’t do that,” I tell them. “You could very well make the same mistake again. It’s helpful to see what didn’t work, as well as the correct answer. I (and your math teachers) want to see the journey you took, including the fruitless paths.” 

Second, teachers ought to present problems that are worthy of their students’ struggle. Ashima Shiraishi has an amazing story of being the youngest person to successfully climb very challenging problems. At the age of 14, she was the first woman (and second person ever) in the world to climb a V15 boulder problem. She has crushed youth competitions, winning several years in a row. When she and illustrator Yao Xaio chose a problem to use for the basis of producing a picture book for kids, they decided on one that was very challenging. Ashima fell many times, having to start over at the beginning. The text shares her process of imaging each place that her fingers or toes would hold as something specific. One was the dot at the end of a question mark. Another was the crook of her dad’s elbow. 

What if Ashima used a simple boulder to illustrate her problem-solving skills? One of the most important themes of the short book would be lost; The idea of developing and practicing persistence couldn’t very well be shared if there were no falls. 

Create fewer math problems that are more challenging. Cause students to have to struggle to conquer each one. If they are required to make memories, it will mean more. If you want your students to “show their work,” give them a problem so complicated that they need to write down notes to get all the way through it. 

The math problem should be a challenging chess opponent in a tournament. Your students should have to show each “move,” as they progress through the solution of the problem. 

There will be practice problems. These are like the rock-climbing walls that Ashima climbs to stay in shape and hone her skills. She will climb the same wall over and over. She will challenge herself to complete the climb faster with each ascent. A story may be imagined for the short climb, and it could be repeated in her head a hundred times, giving the climb life and familiarity. 

This is like memorizing an opening for chess. Increasingly good chess players will learn a variety of initial moves that great players have developed over the years. They will memorize these opening moves through many steps, so that they can anticipate and prepare for potential rebuttals. 

In conclusion, if you want your students to show their work, give them something worthy of writing down the steps it took to complete. Teach them how to make the sharing of their math into a story. In the same way that each move in an important chess game is vital to its end, have students think about what they are doing and share the most important parts of the process. You could even have them try to identify the most crucial part(s) of the problem-solving process. With each boulder of a math problem you give them that challenges their minds and they successfully solve, they should develop a hunger for tackling more and more formidable ones in the future. 

Teaching Ratio

In order to help students understand a concept teachers often have to present it multiple ways. The more challenging the topic is to understand, the more methods might have to be used. I found this to be the case the other day when sharing the idea of ratio with my third graders.

I had presented my Quidditch quandary to the class; “Can a team win a game of quidditch without catching the snitch?” We had explored the ratio of two to one. This had gone fine. My third graders could easily understand the idea of a team being twice as good as another.

I paused at this point and introduced the term ratio. I explained that a ratio described the relationship between two quantities. I made sure that they understood quantity to mean the amount of something; In this case the number of goals a team has in relation to the number of goals another team has. So far, so good.

We worked through several examples of ratios on the board.

They did okay when we changed the ratio from 2:1 to 3:1. Now, one team was three times as good as the other. Things got hairy, though, when we changed the ratio to 3:2.

At first, I tried to just use numbers to show what was happening. “If you used a number that was divisible by three, it’s easier,” I began. “You could put that number on the left side of the colon.” I wrote a twelve on the board. “Then, break it up into thirds. Put two of the thirds on the right,” I told them. “What number goes into twelve three times?”

“Four.”

“Right.” I wrote eight on the right side of the colon… “12:8.” This may as well have been Portuguese to my third graders!

As it turned out, a couple of my students spoke Portuguese fluently! Not literally.

I teach gifted students. That is how I can present problems like these to 8 year olds and expect them to get them. Sometimes, like the present lesson, I have to do some extra teaching. But, for some gifted students, the math comes naturally. It is like a language to them. This is truly remarkable to witness. I captured one of my third grade student’s ratio-realizing moment on video. He used the numbers like a master painter might transition from one color to another. I was so impressed!

He had come up with 48:32 completely on his own. I wanted him to explain where these numbers came from. With a little prompting and help filling in the gaps, he and I recorded his thought process in the video I posted to X.

“I tried 45. Then I got into fifteen because three times fifteen equals 45. Then, I found out that was a tie,” the student breathlessly begins. He started to explain adding three to 45, but I interrupted him.

“How was that a tie?” I prompted.

“To do that,” the student recalled, “You get thirty, which is three hundred,” writing the numbers on the dry erase board as he spoke. “Then you add the snitch, which is 150.”

At this point in the video, I (unfortunately) talk over the student’s explanation. Before I began rolling the video recording, the student had raced through his explanation in his excitement to share his finding the correct answer. I wanted to help him clarify how he new 45 was not the correct answer, before moving on to the right number. With us talking at the same time, the audio is a little cumbersome, but I just kept the feed rolling. “So, show me 48,” I said, giving my student a thumbs up.

The student did not articulate audibly everything he had done, but he showed, through writing on the board, what numbers had been used. He had added three to 45, bringing Team A’s number of goals up to 48. Because 45 divided by three is 15, he knew a number three larger would have a quotient only one more when divided by three. In other words 45/3=15… Raise 45+3 to 48, and 48/3=16.

He instinctually got the relationship (the ratio) that caused each rise by three of the dividend to increase the quotient by one.

It was barely a step for this student to double the 16 to make 32. He then added the value of the Golden Snitch (150) to 320, which is how many points 32 goals would equal.

As the student rewrote his addition on the board, other students watched on. They noticed that the math communicator whom I was video recording had accidentally written “16 X 32” on the board. Someone began to point this out, commenting aloud, “Why’d you write sixteen times thirty-two?”

You can hear me tell this observer, “He’s thinking faster than he can write.” I didn’t want my scholar to lose his train of thought. Some students can be heard confirming that they see how 48 would work. At one point the most beautiful “Ah ha” moment can be viewed when a student realizes how the numbers fall into place unlocking the combination to the problem.

I was very proud of this third grader. It thrilled me to capture his “math talk” on video. Not every student understood the concept of ratio this easily, however. For this student, the numbers and ideas just fell into place. For others, the concept was clunky and the numbers were far from lining up neatly.

I tried guiding them through the same math I had already worked through with my fourth graders. They did fine with the computation, but the third graders were lost when it came to understanding the relationship between the two sides of the ratio. Fractions, multiplication, and division are all relatively new concepts for these students. Even though some of them have been multiplying numbers for years, understanding the concept is not long lived.

In addition to math, we explored the spelling of ratio, after one of my students mentioned that it was a word that did not fit a pattern. “There are other words that do what ratio does,” I mentioned. We brainstormed a bunch.

The students who understood how ratios worked wanted to do more math. They itched to prove themselves masters of arithmetic the way our video star had done. I gave them the new ratio of five to four (5:4), and they jumped on it.

At this point, there were some students who understandably did not know what to do with the five or the four. This was when I took the idea of division and simplified it into forming equal groups to show the relationship between the two sides of the ratio.

“Let’s start off with an easy number,” I suggested. “How about we have Team A score twenty goals.” I wrote a twenty under “Team A” on the board. “If Team A scored twenty goals, and the ratio is five to four, Team B will score more or less?” I figured we could start small.

“Less,” a couple of kids offered.

“Right. How much less might seem tricky to figure out.” The looks on faces told me that they agreed.

An idea occurred to me that I wanted to try. I drew a line of five circles on the board under the number five. I drew four circles under the number four. “What number would you multiply by five in order to make twenty?” I asked. When my students told me four, I wrote the number four inside each of the five circles under the five.

“Remember, ratio means relationship between quantities. That means what we have over here…” I pointed to the five circles with fours inside them, “We must have over here.” I then wrote four inside the four circles under four. “The five fours equals twenty. How much is four fours?” (I know it’s a lot of fours. It feels funny writing four so many times. I contemplated using a different number, but these worked well for [ha ha] my students;)

When they told me that it equaled 16, I wrote that under the four circles. Then, I erased the contents of the circles. I wrote a six in every single circle. “Five sixes equals what?” I wrote a thirty under the twenty. “Four sixes equals what?” Twenty-four got written adjacent the thirty.

An idea occurred to me that I wanted to try. I drew a line of five circles on the board under the number five. I drew four circles under the number four. “What number would you multiply by five in order to make twenty?” I asked. When my students told me four, I wrote the number four inside each of the five circles under the five.

“Remember, ratio means relationship between quantities. That means what we have over here…” I pointed to the five circles with fours inside them, “We must have over here.” I then wrote four inside the four circles under four. “The five fours equals twenty. How much is four fours?” (I know it’s a lot of fours. It feels funny writing four so many times. I contemplated using a different number, but these worked well for [ha ha] my students;)

When they told me that it equaled 16, I wrote that under the four circles. Then, I erased the contents of the circles. I wrote a six in every single circle. “Five sixes equals what?” I wrote a thirty under the twenty. “Four sixes equals what?” Twenty-four got written adjacent the thirty.

One of the students who was working independently had found the answer. When they announced it, we used it to work backward. “What number goes into 80 five times?” With a touch of division we figured out the answer, and I wrote 16 in each circle. “If you have 80 on this side, what number will you have on the other side?” Sixteen times four gives you 64.

To drive home the concept of ratio, I used several other numbers, ending with 500 to 400. “It doesn’t matter how big or how small the quantities,” I explained. “When they are related using the ratio five to four (5:4), they will reflect it by being divisible by five on this side, and four on this side,” I said pointing to the referenced space on the board. “Ratios are easier to understand and work with when we use the smaller numbers, so we reduce both sides to the lowest quotient, using the same divisor. What divisor would we use to reduce 500 to 400?”

While my lesson ended there, here are some ideas for exploring ratios. Compare the land mass between states, countries, counties, or continents. Contrast populations of people or animals.

You could get really scientific with it by exploring the natural ratio between predators and prey. How does nature balance the numbers between the two? Why don’t the predators eat all of the prey? What happens when the ratio becomes unbalanced, and there are too many herbivores? Research the deer population. Find out who is in charge of deciding the number of deer hunters are allowed to kill per season. How do they decide? What would happen if there were many more people getting hunting licenses and more deer than expected disappeared?

Photo by Lisa Fotios on Pexels.com

Investigate invasive species. What causes something to be considered invasive?

Finally, and perhaps more tame, research the ratio of ingredients in dirt. Some plants require more sandy soils. What is the relationship (ratio) between humus, sand, clay, and other materials in your land? This would introduce ratios with multiple numbers. Students could see that when one number goes up, they all do. Double the dirt, and every variable doubles. That is ratio. 

Teaching 2nd Graders How to Draw Conclusions From Data

I was teaching some advanced second graders an enrichment math lesson the other day when I learned something. I often like to mix and combine skills, so that kids can see how math is really used, as well as make it fun. At the end of this particular lesson, I used the data we had collected throughout our time together to summarize what had happened. As I attempted to make sense of the numbers, I found myself making conclusions or at least forming a hypothesis that could be tested. When I pointed this out to my second graders, I thought to myself, “Wow, this is a pretty good lesson I’m learning right now.” I was thankful that I hadn’t stopped at only having my students do the original lesson’s math. 

The lesson involved making estimates and then measuring actual length to the nearest inch. The first thing I did was model. I took a wooden block out of a box; my “Box o’ blocks”!  After standing it up on the table, I asked, “How tall do you think this is?” I received some wild guesses from my second graders. Someone thought it might be a foot. Another student said two inches. 

I picked up the block and measured its length with a little mini ruler. I showed the students where the block ended on the ruler. They eventually settled on the idea that the block stopped between the five and the six. One of the students suggested that it was five and a half. 

After praising this smarty, I asked them if it was okay to measure the block laying down, because I was holding it flat in my hand. We were supposed to be measuring its “height.” Their spatial reasoning skills were sound, and we all agreed that we were measuring the length of the same side, no matter which direction it was facing. 

After teaching estimating and measuring and before breaking the group up into teams, I explained the directions. Each team would get some random blocks. They were to work together to build a tall tower. It had to be free standing; No holding it. Every block should be used. I would give them two minutes to construct the tower. When the timer goes off, the teams will form an estimate of how many inches tall the tower is. Once the team has decided on a number and communicated it to Mr. Weimann (me), they get a yardstick to measure the actual height. 

I would be keeping track of our estimates and accurate measurements. The idea was to try to get your estimate as close as possible. 

Next, it was time to form teams. I just had kids who were sitting near each other form teams to make it go faster. I dumped random blocks in front of each group and told them to get started. After the first two minute timer sounded, I stopped everyone. I had the groups come up with estimates of how tall their towers were. As each team shared their estimate, I had them provide a name for their team, as well. Clowning around, I purposely misspelled the names they gave me. That had them laughing. 

After I wrote the estimate under a team’s name, I handed them the yardstick. Watching them estimate the height was fascinating. One group had a girl who used two fingers squished together to climb the tower with the members counting as she jumped. They figured her fingers constituted about an inch. They were very accurate. Another group had a student using his arm, presumably thinking it was a foot long. After a round or two I reminded groups that the medium sized block was already measured. We found it to be exactly five and a half inches tall. They could use that in their estimates. I don’t think any of them did, but we can revisit that. 

As it turned out, we only had time for three rounds. After collecting all of the wooden blocks, I went over the chart that I’d made. I had second graders figure out the difference between each estimate and measurement. I wrote that data on the board in a different color. We then added all of the differences from each team together to total them on the bottom of each column. Although two teams had the same total, three inches , one of them had never supplied any data for one of the rounds; Their tower kept tumbling, and they were never able to estimate or measure it. 

We had more than one type of winner.

The “BeeKays” began rejoicing for having the largest total, presumably the winners, but other second graders squashed their victory dance with unwelcome information. Like golf, the total that is the smallest was winner. It took a little convincing, but I explained that the goal was to get the estimate as close as possible to the actual measurement. The smaller the difference, the better the estimate. “Look, the very first round had a team whose measurement ended up being exactly the same as the actual measurement! The difference between the two was zero. This zero was the winner of that round.”

Next, was the very cool part for me. Here is where I joined my students in learning, albeit through teaching. I had asked the students what data was. They eventually settled on the synonym, “information.” I added to this the word “useful” and proceeded to show them how we could use the data to draw conclusions. The team that had thought they won because the sum of all of their differences was the greatest, eleven and a half, did actually win something. They were the winners of which team improved the most. 

“What do you notice when you compare the differences of each tower they built?” I asked the group. “They got smaller and smaller. The first tower was estimated to be eight inches shorter than it actually was. The group over corrected a little on the second tower, estimating it to be a little taller than it was, but only by three inches. The final tower was within half of an inch of its estimate!” I pointed to each difference on the chart as I explained its meaning. “The estimates got more and more accurate, as the BeeKay team practiced.” I let that sink in. 

After pointing out that the data shows some improvement in the other two groups, it isn’t as consistent as the middle group’s. As I time ended, I taught my second graders that we just analyzed data and developed conclusions based on the information we collected during our lesson. “What might we expect to happen if we built some more towers and continued this exercise of estimating and measuring?” I asked. 

Hands shot up all over the room. “They would get closer and closer,” someone shared. 

Putting it into mathematical terminology, I restated, “That’s right. The differences between the estimates and the measurements should get smaller and smaller as you get better at estimating.” 

Teachers use data all of the time to measure how students are doing. Do you ever show students how the data works? Give it a try. 

Making Math Connections: 1st Grade Double-Digit Addition

Snargg and Plory, iReady mascots

Yesterday, I had the privilege of attending a one-day conference hosted by Curriculum Associates, the company that produces the lessons that I use to teach my students math. During a whole-group general session between breakouts a few different leaders from the company got on stage to share some ideas. One of them was Kenneth Tan. He was in charge of speaking about some new ways of interpreting the data that diagnostic assessments provide.  

He did a nice job making meaning from graphs and charts. One of the things that Kenneth shared caused me to remember a lesson I’d taught my 1st grade math enrichment class the day before. 

Keynote speaker Glendaliz Almonte shares in Grand Ballroom Hilton Philadelphia at Penn’s Landing.

He had an image appear on the huge screen at the front of the room. It was a grid with around 12 or 16 seemingly random words in boxes. The audience was asked to try to remember as many words as possible. I figured there was a catch, and I took a couple of seconds to glance over the entire grid, getting a feel for the words. Were there any connections that could be helpful?

Just as I realized that the collection of words contained not only nouns and verbs, but adjectives and articles as well as prepositions, the image disappeared! I tried to quickly string together any words I’d remembered, forming a sentence, no matter how silly. 

The speaker probably knew his audience was smart enough to think of this trick and, either to limit their success or to save time, switched slides from the grid of random words to one containing the sentence that I’d tried to piece together. Kenneth Tan remarked that data is only as helpful as it is meaningful. I liked the analogy. 

The idea of connecting words made me remember my first grade math enrichment lesson from Monday. In that lesson, I had students join single-digit numbers to grow a double-digit number from the left side of the image larger and larger, until it eventually equaled the double-digit number shown on the right. This lesson was straight out of the Ready Math Teacher Toolbox (Lesson 20).

With the image imported into a Jamboard, students were able to trace over the provided lines with color. Each color was a different student’s work.

Typing out the process makes the lesson seem more complicated than it was. As you can see from the image, Ready Math had numbers in boxes. Some were double-digit, and some were single-digits. The double-digit numbers flanked the single-digit numbers. Students had to leap frog across the boxes with numbers to get from one double-digit number to the other, and the trip should create a balanced equation. Ready Math had an example that made the task plain as day.

The activity was an instant hit! Among other things, we discussed the relationship between the numbers. The 17 needed a nine to get it to 26. There were several ways to make nine, using the numbers that were available. We talked about combinations of numbers that could not work, and why, as well. One student (the blue line and numbers) wanted to go from 17 to nine, and then visit eight. Either they wanted to try something different, or they had recognized that eight plus nine equals 17. I let them try it, but they realized that the path would not “land them on” 26. They would over shoot their goal.

The Ready Math enrichment assignment had a few diagrams with varying numbers. I had different students come up to the Google Jamboard to draw paths and write equations that demonstrated getting from one double-digit number to the other.

I showed the first graders that every equation for a diagram had some parts that were the same. The first number, the double-digit number, was always the same. And, the sum, the double-digit number on the other side of the equal sign is the same for each. It is the middle addend(s) that change. To illustrate this fact, I drew two boxes in the middle of the equation. These symbolized the boxes from the diagram that held single-digit numbers. When we had finished working through the numbers that were available, we came up with some others that weren’t shown.

Then things got really interesting. The first graders felt bothered when one of the diagrams had numbers that were not being used. The starting number was 88, and we had to get to 95, a difference of seven. One of my students drew a line from the 88 to an eight. That would put the running total up to 96, one past the goal of 95. Rather than tell the student that he was wrong, I asked if there was anything that he could do to “Balance the Equation.”

With a little help from his friends, the first grader decided to change the operation from addition to subtraction between the single-digit numbers. In this way, he was able to incorporate the last unused number, a one. Sure, one had to be “taken away” in order to complete the algorithm accurately, but at least he was valued worthy of a place in our equation!

More than adding and subtracting, this was a lesson in making connections and building relationships between numbers. Finally, finding balance between the two sides of the equal sign is not just algebra. It is a life skill.

Developing Real-World Math Problems: Adding & Subtracting Mixed Numbers

During an interview for a podcast with Curriculum Associates the other day I was asked how I use real world scenarios to enrich math lessons. I had explained to the interviewer that teaching is a second career for me. My experience of entrepreneurship as a residential custom painting contractor helps me introduce loads of business expertise in my math lessons. 

Blog about using tile cutting in a math lesson
Blog about using wallpaper hanging in a math lesson

The interviewer was looking to provide practical solutions for teachers to use. I took two seconds to imagine I was sitting in front of my computer (as I am right now;) and tried to remember the steps of making my lessons. 

The first thing I do is find the lesson in the i-Ready toolbox, and look at the “Extend Learning” assignment. I don’t usually use the i-Ready assignment verbatim, just in case the regular education teacher wants to assign it. I use it as a guide for my enrichment lesson. 

i-Ready provides paper lessons that can be assigned virtually or printed out.

For instance, this week my fourth graders were learning about adding and subtracting mixed numbers (Lesson 21). The extended lesson shares a story about a couple of kids filling a fish tank. Some mixed numbers are used, and kids are asked to do calculations that would require them to add and subtract the mixed numbers. 

Here’s a GIF I made showing our classroom 75 gallon fish tank. I made the stand that it is sitting on out of 4 X 4s.

I actually have a 75 gallon fish tank in my classroom, so this story could very well be perfect. However, I just wasn’t feeling the mixed number connection. There is no way that three friends would have three different buckets that all hold different mixed numbers of water with a fraction containing the same denominator. It felt too implausible. 

Regular Ed teachers could still use this paper assignment about students using mixed numbers to fill a fish tank.

I sat at my computer and thought, Where do I encounter mixed numbers? In addition to having run a successful business, I’m also a “Do it yourself-er.” I enjoy building things. Making things with my own hands and tools is satisfying to me. I made the stand that my fish tank sits on. I finished my own basement, complete with bathroom and laundry room. In short, I have come across plenty of mixed numbers! Developing an enrichment math lesson that uses mixed numbers will require me to make the work of adding and subtracting the mixed numbers both doable and easy enough for the fourth graders to understand. That is my challenge.

When I say that I like to use my hands to build things, I don’t mean paper airplanes. Check out this blog about my giant wooden sunken pirate ship classroom decoration.

The morning that I came up with “Fix a Bench” my first thought was to have my students figure out how many boards would fit on a small deck surface. Each board could be a mixed number in width. This would be similar to the fish tank assignment from i-Ready. Kids would just add them up to fill the space.

As I began researching and looking for pictures online to jazz up my presentation, I remembered that lumber is full of mixed numbers. The most common building material, the two by four, is NOT really two inches by four inches. I learned this ages ago when I expected several adjacent two by fours to equal a nice even round number. It was some wacky measurement, and I took a closer look at the dimension of the studs (two by fours) I had purchased. I was incredulous, thinking I’d been ripped off! 

Thinking this might be a fun fact to share with my students, I decided to have them explore having to use various sized pieces of lumber to make something. The fourth graders love mysteries, and I would wait until the very end to explain why two by fours are called that when they actually aren’t those dimensions. 

My lesson was originally “Build a Bench.” When I began planning what my students would actually do, however, I figured out that it would be easier to teach and explain if I had them only choose lumber to place onto an already existing frame of a bench. Thus “Fix a Bench” was born. 

The next part of developing a good real-world lesson is to create a “Sell.” You must come up with a pitch to draw the students in. “Today we’re going to fix a bench” isn’t good enough. Instead, I told my students that “It’s your parents’ anniversary (or birthday for single-parent families), and you want to give them something, but you have no idea  what! They have a special bench that they like to sit on, but the wood is rotting. You get the idea that you will fix this bench for them as a gift. Because you don’t have enough money to buy the wood to do the work, your parents agree to get it for you. Your labor and thoughtfulness is the present. In exchange for your parents footing the bill, you have to tell them exactly how much the lumber will cost.”

This little story makes sense to the students. Even if they don’t have a bench in their backyards or don’t have a backyard at all, they can imagine doing this kind of thing. Also, it gives them some good ideas of how to come up with presents for their parents that won’t cost them anything more than creativity and thoughtfulness. 

“How much does the wood cost?” the students instantly want to know. 

“Before I tell you the costs, I am going to need a helper… This person has to have very good penmanship. I will know that they can write very neatly by how well they listen to the explanation of the project…” I share this with a very stern look in my eye, as I scan the room for anyone not paying close enough attention. Every student straightens their body and widens their eyes. I proceed to share the dimensions of the bench frame.

I got the size of the bench by measuring one of the chairs in my room. The back was approximately 16 inches tall, and the seat was 14 inches deep. Instead of supplying these simple numbers, I turned them into mixed numbers. Sixteen inches turned into 1 ⅓ feet, and 14 inches transformed into 1 ⅙ feet. In order to narrow the focus of calculations, I made the bench exactly eight feet wide. This way, there wouldn’t be any trimming of the ends of the boards. Just choose eight foot long pieces. 

Now, it was time to show the students the materials available to them. I had found a list of lumber online that showed the names of the wood with the actual dimensions next to them. With this image on the screen in front of the class, I showed students how a two by four is actually 1 ½ inches by 3 ½ inches. A two by six, another common board measurement, is really 1 ½ inches by 5 ½ inches. And, a two by eight board is 1 ½” by 7 ¼”! 

The class needed a little guidance to get started with this lesson. I guided them through drawing a diagram of the important parts of their bench. We labeled the back, the seat, “And don’t forget about the single board that goes on top!” I told them. I had them figure out how many inches the mixed numbers would translate to. “Now, we have to fill these spaces (16 and 14 inches, respectively) with lumber,” I told them. “It would be easy if two by fours were actually two inches by four inches, but they aren’t! See if you can figure out how to make sixteen inches of surface using these mixed numbers.” I circled the widths of the “two bys” from the image. I had told them that we would only use those, because they need to be thick enough to hold a human’s weight. 

Using only 3 ½ (the width of a two by four) won’t work for the back of the bench. My students figured out that four of these boards will get you to exactly fourteen inches of wooden surface. That leaves you with a two inch gap, and “We don’t want any spaces. Neither can we saw any boards to resize them. There aren’t any boards that are exactly two inches wide. Can you take away one of the two by fours, and find a different size board that fits nicely?” 

When my students take 3 ½ away from fourteen, they have 10 ½”. “What is the size of the space, now?” I ask this while pointing to a gap that I’ve illustrated on my drawing of the bench we are fixing. They figure out that the empty space is exactly 5 ½ inches wide. “Are there any 5 ½” wide boards that we can purchase?” Yes. The 2 by 6 is that width. 

Are we done? Definitely not! “You were all such hard workers and very good listeners that it is very difficult to decide who could be my writer,” I tell my class of math enrichment fourth graders. 

One of the students actually volunteered another, saying, “Nahum has really good hand-writing. You should have him write on the board.” 

“Are you nominating your friend?” I inquire. He admits it, and several students second the nomination, suggesting that Nahum really does have good handwriting. “Well, okay, then. Come on up here,” I extend the invitation and commend Nahum’s friend for being classy.

As Nahum prepares to write on the board, I open my laptop. I have pricing from a lumber yard ready to go. We now write down the amount of money each board will cost us. I have Nahum give the writing tool to other kids after he writes a couple of prices, so that more students get a chance to write on the board. We only supply the prices of the two-bys, because those are the only ones we are using. 

Students proceed to figure out the cost of 3 two by fours and 1 two by six. When they think that they are done with the project, I point out that we still have to figure out the seat of the bench. They happily begin problem-solving that challenge independently. It took a surprising amount of time for them to figure out that we had already answered the question of what boards could be used. The 4 two by fours that we had added up earlier had totalled exactly fourteen inches, which is the size of the seat! 

When they began adding up four prices of two by fours, I pointed out that we already knew how much three of them cost. “Why not just add the cost of one more to the first number?” I suggest. Grateful for the idea, they do this. 

Preempting the “I’m dones!” that were about to fill the room, I reminded them, “Don’t forget about that top board… The one that goes on the top of the back of the bench.” Happy groans and more pencil scratching ensued. 

Just when my students thought that they were finally done, and Mr. Weimann couldn’t come up with any more surprises, I told them, “It would be very classy if you figured out how much your parents would have to pay in sales tax.” Epic groaning accompanied smiles and students beginning to hunch over their iPads. I told them to use calculators and that our state sales tax was six percent. This was the icing on the cake. 

After a few seconds, I modeled for them, asking Siri, “What is six percent of thirty-eight dollars and fifty-six cents?” When she told me, I wrote it on the board for them. 

Because I had created Google Jamboards with all of the information preloaded on them, I was able to see each individual students’ work. I had waited until Nahum and partners had neatly written the prices into the slide with lumber details before I pushed the Jamboard out in a Google classroom assignment. I had the software “Make a copy for each student.” Students knew that, although they were allowed to work with partners and I helped them solve several parts of the problem on the board, they had to add their own version of the details, showing their work

Before students left my room I explained why two by fours are actually mixed numbers. The lumber is cut at exactly two inches by four inches, but when it dries, it shrinks. Of course the students wanted to know why lumberyards don’t correct for this or call the wood by another name. The young minds cried foul and felt tricked! I told them that it has been this way for a long time, it is easier to say “two by four” than “one and a half by three and a half,” and the price of the wood that you feel like you are being cheated out of goes into having to store it while it dries, before selling it. It isn’t like the mill cuts a two inch by four inch pied of wood for you to bring home, you build with it, and it shrinks on your home. That would be worse. In the same way that creating this lesson required several steps, when one wants to make and use a two by four, you measure the wood, cut the lumber, let it dry, measure it again, and then you can work with it.

Communicating Creative Mental Math Verbally

“I don’t know how I got it; I just know that this is the answer,” a frustrated student defends himself against the inquisition of an even more frustrated teacher who wants him to “SHOW YOUR WORK!”

You should have seen the students’ eyes bulge when I told them I was going to give them candy! LOL They were happy to gobble up the math, though.

But, what if he actually doesn’t know where the number came from? We don’t ask the toaster to “Show us how it heats up our bread.” When was the last time you insisted that the mechanic “Show you HOW they fixed your car”? (They always try to explain it to us, and I’m like, “Does it work? How much does it cost? I got stuff to do.” Ha ha;)

I recently had a math enrichment lesson with second graders where I told them what they didn’t know they did with a couple of mental math problems. We were working on comparing three-digit numbers. I had printed pictures of snacks that had prices on them. Teams of students were first asked to arrange the snacks in order from least to greatest price. Then I asked the class to compare the cost of three items to the cost of two others. The students didn’t have paper or anything to write on. 

Please pardon my penmanship;)

After I received some successful answers, I asked the teams, “What did you do in order to produce those answers?” I got a variety of responses. Most teams told me the names of the operations. “We added the three numbers together, and then subtracted…”

One group explained what they did to complete the operations, and I was very impressed. While students were sharing, I took some notes on the board. I clarified what the group was communicating by drawing circles around numbers and pulling out concepts.

“You began by adding 65 cents to 55 cents,” I reiterated. Nods of heads confirmed the accuracy of my statement. What happens in a creative mathematician’s head is a little different from what one would do on paper, however, and I wanted to pull this out. These students hadn’t used an algorithm.

I like to do a lot of mental math in my room, because it helps kids develop number sense. “The 65 and 55 are both pretty close to a number that is really easy to add in your heads,” I told them.

Here’s a post that shows 3rd graders communicating the use of compatible numbers to multiply.

“Fifty!” the group called out. We have been identifying compatible numbers, so they already knew to look for something more manageable.

“That’s right. And, in order to get to fifty, you have to adjust these a little.” I circled the 65 and wrote 15 on the side. Then I circled only the 5 from the ones of 55, and I wrote that near the 15.

If a student had paper in front of them, they might line up 65 and 55. Then they’d add the fives from the ones’ column and regroup with a “one” above the tens column… But, do we grown ups do this in the grocery store when we are comparing one item with another? No, we use mental math. We develop creative tricks that we may not even realize we use!

My aim is to unlock this mathematical creativity early in life. A secondary goal is to help students be able to communicate it.

“After adding the two 50s together, what did you do?” Everyone can see that there is still a 15 and a 5 written on the board. I wrote the sum before anyone called out, answering the rhetorical statement myself. “Now, you need to add this $1.20 to 99 cents. That sounds hard,” I teased, knowing that they’d already smashed that algorithm in their minds.

Letting students work in teams allows them more than just Social Emotional Learning (SEL). They help one another remember and recall sums and differences.

When I told them about using 100 instead of 99, several students silently shouted, “That’s what I did!” No one is going to carry a one from the tens to the hundreds column of a mentally constructed algorithm. And, we don’t always have paper. AND, do you really want to teach your students to be dependent on paper?!

Now, think about it, reader. Students are using subtraction in order to add numbers together. What 8 year old is going to be able to explain this abstract use of arithmetic in writing on a test or assessment?

Here, I’m having the group of 2nd graders “play” with numbers by lining their teams up in order of least to greatest, having constructed the largest number possible with the loose number cards I’d given everyone in each team. Get-up-and-move-around-math.

And, we (myself included) expect them to “Show their work!” I’m happy if they know what they are doing and get the correct answer. I’m nearly 50, and I only just learned how to show MY own work! LOL

What I found myself doing in the past was asking students who had performed mental gymnastics to achieve a remarkable mathematical feat to write down the steps they took. In other words, if you added up three numbers (65 + 55 + 99), and then subtracted a fourth from that sum, write it all down…

Even if you can’t describe the exact process of creating the sum or exactly what you did to subtract. Just tell me what you did with the numbers. I, like every other math teacher in the world, wanted to see more than just an answer!

I think that having students use mental math, and then having them explain what they did VERBALLY is helpful in sharing the mechanics of the creative math. It’s easier to verbalize than it is to write. I bet there are books written about this. (If you know of any, please share. Thank you.)

A tool I’ve enjoyed having students use to verbally communicate their creative math skills is Flip (formally known as Flipgrid). Kids can make videos of themselves talking about the math. They can also write on their screens to show what they did while talking about it. If they did the math on paper, they can take a photo of their work to include in their video. Finally, they can watch each other’s videos, get ideas for future creative math projects, and leave encouraging replies to each other. The platform is easy to navigate and teacher-friendly for leaving feedback and assessment info.

In conclusion, while I always instinctually knew that forcing a kid to write down everything they did in their head could squash their creativity, I never knew how to bridge the gap between teacher and student; The chasm between the answer (what the student produces) and the process (what the teacher cares most about) before now. I’d tried varying techniques with varying results. My new thing is to verbally walk them through tricks I’d use to do mental math. Through this process, they recognize some of what they are already doing in their minds. They are learning how to communicate it. And, some students are learning creative ways to play with numbers.